
O físico austríaco Wolfgang Pauli (1900-1958) foi um célebre resmungão. Quando assistia às palestras de seus colegas, costumava classificar as ideias em falsch (“errado”, em seu alemão nativo) ou ganz falsch (“muito errado”). Certo dia, um colega lhe trouxe um artigo de um jovem físico e pediu sua opinião. A resenha de Pauli teria sido nicht einmal falsch – em português, algo como “nem chega a estar errado”, ou “nem sequer errado”.
Embora a história seja apócrifa – não há qualquer evidência de que Pauli tenha dado esse coice específico –, a piadinha expressa o que muitos veem como uma característica central para o método científico: se uma hipótese não pode ser comprovada ou refutada por meio de experimentos ou observações, então ela está fora da alçada da ciência, em que todas as afirmações precisam ter algum tipo de relação com a evidência empírica.
Ou seja: Pauli não quis dizer que as ideias do jovem físico estavam erradas porque vão na contramão do que se observa na natureza (o que renderia apenas um falsch ou ganz falsch). Na verdade, o ponto é que Pauli não via uma maneira de comprovar ou refutar as afirmações feitas pelo rapaz.
O físico matemático Peter Woit, professor da Universidade Columbia, em Nova York, transformou a frase de Pauli no título de seu livro Not Even Wrong, lançado em 2006. A obra é uma crítica à teoria de cordas, uma área cabeluda da Física que alcançou os holofotes na década de 1980 com a promessa de resolver o maior impasse da ciência contemporânea: a incompatibilidade entre a mecânica quântica e a teoria da relatividade geral, que são os dois pilares da nossa compreensão do Universo.
Em diferentes momentos das décadas de 1980 e 1990, a teoria de cordas angariou um enorme número de pesquisadores esperançosos com seu poder explicativo, e vários deles permanecem na área até hoje. O físico teórico Cumrun Vafa, da Universidade Harvard, chegou a afirmar que “a teoria de cordas está permitindo o mais profundo entendimento do Universo que jamais tivemos”.
Porém, na opinião de Woit e outros personagens do debate atual, a teoria de cordas não só passa longe de alcançar seu objetivo de unificação como acabou se tornando um monstrinho matemático de complexidade intransponível, que engole verbas de pesquisa à rodo, desperdiça bons talentos na pós-graduação e é incapaz de gerar previsões verificáveis. Em suma, uma teoria que “nem sequer está errada”, mas ganhou ares de fenômeno cult.
Vamos entender a discussão, começando pelo impasse, explicando como a teoria de cordas se propôs a resolvê-lo e os problemas que ela não conseguiu superar ao longo das últimas quatro décadas. O primeiro passo é explicar em que pé está nossa compreensão das partículas que compõem o Universo – e das forças que regem a interação entre elas. Nas palavras de Bill Bryson: “A Física nada mais é que a busca pela simplicidade definitiva, mas, até agora, tudo que temos é uma espécie de bagunça elegante”.
O estado atual
A receita do Universo é razoavelmente simples. Vamos começar arranjando algumas coisas para ocupá-lo. Coisas como pessoas, ou cachorros, ou planetas, ou galáxias inteiras. Para isso, precisaremos de três partículas fundamentais chamadas quark up, quark down e elétron. Por “fundamentais”, entenda: esses são tijolinhos indivisíveis; unidades mínimas da matéria. Não podem ser decompostos em nada menor.
O primeiro passo é juntar os quarks para formar partículas mais gordinhas chamadas prótons e nêutrons. Depois, precisamos misturar prótons e nêutrons com elétrons para formar átomos. Átomos, você sabe, vêm em vários tipos: oxigênio, hidrogênio, carbono etc. De fato, é só mudar o número de prótons para obter qualquer elemento da tabela periódica. Ótimo, temos a matéria-prima necessária para fazer coisas. Todas as coisas.
Só que não. Misturar partículas não é tão trivial quanto mexer uma massa de bolo. Alguns problemas vão emergir. Por exemplo: os prótons têm todos carga elétrica positiva, e por isso se repelem. Isso é cortesia da força eletromagnética, uma das forças fundamentais da natureza. (Pensando em termos de partículas, os físicos dizem que a força eletromagnética tem uma partícula mensageira chamada fóton, e que quando os prótons estão se repelindo, eles na verdade estão trocando fótons entre si, que transmitem o recado do afastamento. Esse detalhe é supérfluo agora, mas se tornará relevante daqui a alguns parágrafos.)
Como convencer os prótons a se manterem juntos para formar átomos? Você vai precisar de uma nova força da natureza, chamada força forte. Ela combate a força eletromagnética, mantendo tudo coladinho no lugar. Por isso, a partícula mensageira da força forte se chama glúon – sim, o nome vem de glue em inglês, que significa “cola”. No núcleo do átomo, o recado do glúon fala mais alto que o recado do fóton.
Continue os esforços de construção de um Universo e logo ficará claro que o manual de instruções não faz muito sentido. Por exemplo: você logo vai descobrir que o elétron precisa ter dois sósias mais pesados: o múon (µ) e o tau (t). Esse par de partículas coadjuvantes também têm carga elétrica -1 e ambas seriam indistinguíveis dos elétrons comuns não fossem suas massas, que são respectivamente 200 e 3 mil vezes maiores.
Partículas como múons e taus não têm um papel relevante na formação da matéria comum, e sequer há uma explicação satisfatória para o fato de que existam da maneira como são. São como peças de Lego sobressalentes, que vieram na caixa mas não servem para montar praticamente nada.
Eles não participam do seu dia a dia e costumam aparecer apenas em fenômenos naturais que envolvem altas energias, como a colisão de raios cósmicos com a atmosfera terrestre – ou em experimentos complexos e caríssimos, projetados especialmente para detectá-los (como os realizados no Grande Colisor de Hádrons, o LHC, em Genebra – um dos túneis do LHC ilustra este artigo). Quando os múons foram descobertos, em 1936, o Prêmio Nobel Isidor Rabi (1898-1988) coçou a cabeça, incrédulo: “Quem encomendou isso aqui?”
Os quarks up e down também têm duas versões sobressalentes cada um, cópias tão aparentemente desnecessárias quanto são os múons e taus, mas cuja existência já foi verificada em experimentos.
Esse grande zoológico de partículas que se esconde na escala microscópica é descrito pelo chamado Modelo Padrão, uma espécie de tabela periódica do mundo subatômico, que lista as características das 17 partículas fundamentais. Nele estão elétrons, múons, taus, os seis quarks, os fótons, os glúons e uma porção de outras partículas que podem ser mais ou menos importantes para a existência do mundo como o conhecemos. Veja abaixo:
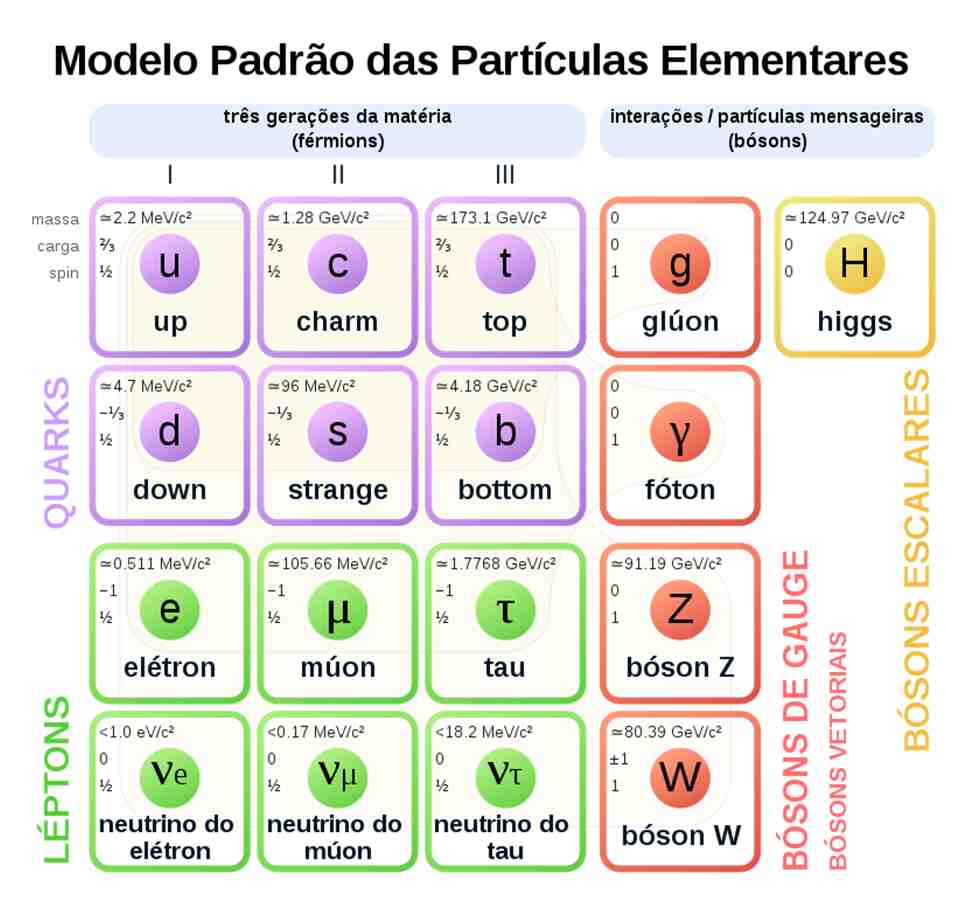
O Modelo Padrão se estrutura em torno das teorias quânticas de campos (quantum field theories, QFT), que são uma expansão do trabalho iniciado com a mecânica quântica no começo do século 20. Esse arcabouço matemático que descreve o mundo microscópico é, de longe, a coisa mais precisa já criada pela civilização. Hoje, somos capazes de calcular dados como o spin de um elétron com doze casas decimais, o que equivale a determinar a distância entre o Oiapoque e o Chuí com margem de erro de um fio de cabelo.
Essa precisão ridícula torna o Modelo Padrão o arquétipo de uma teoria científica bem-sucedida, verificada experimentalmente acima de qualquer dúvida. Mas isso, você já deve ter percebido, não significa que ele não tenha suas limitações. O físico teórico Lee Smolin, do Perimeter Institute no Canadá, resume algumas delas.
Uma é a questão dos ajustes finos: não sabemos por que o elétron tem tal massa e tal carga elétrica, enquanto o múon tem outras, e os quarks têm outras etc. As partículas simplesmente são do jeito que são. De fato, já comentamos que não há um bom motivo para quarks e elétrons terem gêmeos mais pesados. O Modelo Padrão se compromete a explicar como o mundo funciona, mas não diz por que ele é assim.
Isso dialoga com o problema dos parâmetros livres: o Modelo Padrão é estruturado em torno de 19 números que precisam ser obtidos experimentalmente. Você pega o elétron, múon ou quark, mede o dito-cujo e consegue o valor de que precisa. Esses números não emergem como resultado de nenhuma manipulação das equações; são pré-requisitos para a existência da teoria. Uma explicação para o Universo mais abrangente do que o Modelo Padrão poderia ser estruturada de tal forma que esses números emergissem como consequência de princípios subjacentes mais simples.
A relatividade geral
A seção anterior foi toda dedicada a explicar como preencher o Universo com coisas, mas não falamos sobre o Universo em si. O que é, exatamente, o espaço tridimensional em que todas essas coisas existem? O que é o tempo?
Nossa compreensão atual do tecido do Cosmos – do cenário em que os atores do Modelo Padrão atuam – vem da teoria da relatividade geral de Albert Einstein (1879-1955), publicada em 1915. Einstein tratou o espaço e o tempo como uma espécie de rede flexível, um grande tabuleiro em que se apoia a realidade. A massa de corpos como estrelas e planetas deforma o espaço e o tempo, da mesma forma que seus pés deformam a superfície de uma cama elástica.
Quando algo massivo deforma o espaço e o tempo, a trajetória dos corpos ao redor é alterada – afinal, as coisas se movem no espaço, e se o espaço muda, o movimento muda também. A esse fenômeno damos o nome de gravidade. A Terra se move no espaço-tempo deformado pela presença do Sol. E você se move na deformação menor causada pela presença da Terra.
O problema é que as equações da relatividade geral pertencem à física clássica e não dialogam com as da mecânica quântica. Essa descrição geométrica da gravidade, baseada na curvatura – deformação – do pano de fundo do Cosmos, é matematicamente incompatível com o tratamento que os físicos dão para as outras forças da natureza, como a força eletromagnética. Tanto é que nunca se detectou a partícula mensageira hipotética da gravidade, o gráviton.
Por isso, a maioria dos físicos pensa no trabalho de Einstein como uma aproximação muito bem-sucedida, e espera que, no longo prazo, a gravidade receba um banho de loja quântico para se integrar ao Modelo Padrão, com direito a sua própria partícula mensageira.
Essa incompatibilidade é tolerável na maior parte do tempo porque os objetos de estudo das duas teorias não se cruzam. Os astrônomos e astrofísicos empregam a Relatividade Geral para compreender fenômenos em escala cósmica, como ondas gravitacionais ou estrelas de nêutrons, em que a curvatura do espaço-tempo tem um papel central. Por sua vez, a turma do Modelo Padrão se dedica a investigar as partículas fundamentais e as maneiras como elas transformam-se umas nas outras, após as colisões de altíssima energia em aceleradores de partículas.
O bug começa nas situações em que as duas teorias precisariam se unir para fornecer uma explicação satisfatória. É o caso da singularidade no centro de um buraco negro. As equações de Einstein indicam tratar-se de um ponto sem dimensões, infinitamente pequeno, em que se concentra toda a massa remanescente do núcleo de uma estrela que desabou sobre si mesma. É improvável, porém, que essa explicação esteja certa: precisaríamos de uma teoria quântica da gravidade para explicar o que ocorre com um gigantesco bocado de matéria espremido em um espaço tão diminuto – diminuto o suficiente para entrar no domínio de conhecimento dos físicos de partículas.
Virtudes e problemas
A teoria de cordas parte da premissa de que as partículas fundamentais do Modelo Padrão não são pontos destituídos de estrutura interna, mas sim minúsculas cordas unidimensionais. Essas cordas vibram como as de um violão, e padrões vibratórios diferentes resultam em partículas com características diferentes. É como se múons, elétrons ou quarks fossem notas musicais diversas tocadas pelo mesmo instrumento.
É crucial destacar o salto explicativo que essa hipótese representa. Lembre-se: o Modelo Padrão não fornece um motivo para o elétron ter uma massa e o múon ter 200 vezes essa massa. Eles são assim, diferentes, por princípio. A teoria de cordas, por outro lado, resolve a questão afirmando que elétrons e múons são só modos de oscilação diferentes da mesma coisa. Nesse arcabouço teórico, existe um único tipo de matéria-prima em todo o cosmos, que são as cordas. Todas as diferenças verificadas entre partículas, em última instância, se resumem às diferentes maneiras como esses filamentos se agitam.
Um desses padrões vibratórios corresponderia ao gráviton, e eis o trunfo da teoria de cordas – a esperança de que ela seja uma teoria unificadora, capaz de explicar, por exemplo, a singularidade do buraco negro. A gravidade deixaria de ser um empecilho para se tornar só mais uma nota da sinfonia cósmica. Lindo.
O problema começa quando descobrimos que esses elásticos hipotéticos teriam comprimentos na ordem de grandeza da distância de Planck, que exige 35 zeros depois da vírgula para ser expressa em metros. Estamos falando de uma escala 100 milhões de bilhões de vezes menor do que a observável pelos melhores equipamentos atuais.
(O físico israelense Shmuel Nussinov, diga-se, já calculou que um acelerador de partículas com energia alta o suficiente para verificar, em primeira mão, a existência das cordas precisaria ter o diâmetro do Universo, de modo que os físicos experimentais podem esperar sentados por uma comprovação empírica direta.)
A elegância aparente da teoria escondia ainda monstrinhos matemáticos difíceis de domar, que foram aparecendo conforme as pesquisas na área avançaram – e que, por enquanto, impedem a teoria de gerar previsões certeiras, passíveis de confirmação empírica. Nas palavras do teórico de cordas Brian Greene, ele e seus colegas são como crianças com um brinquedo espetacular em mãos, mas incapazes de usá-lo em todo seu potencial, porque o manual de instruções está incompleto.

Um desses problemas é que a teoria de cordas só funciona se as cordas em questão puderem vibrar em nove dimensões espaciais. Ou na verdade, dez: uma dimensão extra precisou entrar em cena quando Edward Witten, da Universidade Princeton, realizou uma grande unificação de cinco diferentes versões da teoria de cordas, em 1995.
Todos nós podemos verificar que o Universo conhecido tem três dimensões, o que leva à pergunta: onde estão as outras seis – ou sete? A explicação é que essas dimensões extras permaneceriam recurvadas e ocultas, dobradas sobre si mesmas na minúscula escala de Planck, e tão invisíveis aos equipamentos disponíveis hoje quanto as cordas em si. Por isso, verificá-las na prática permanece uma meta distante.
Melhor ainda: as dimensões extras ficam dobradas e compactadas de acordo com construções geométricas extremamente complexas chamadas formas de Calabi-Yau, que são objeto de estudo da vanguarda da matemática. Em princípio, o fato de que as partículas do Modelo Padrão aparecem agrupadas de três em três poderia ser explicado caso as cordas vibrassem dentro de um tipo específico de forma Calabi-Yau, com três buracos. Cada forma de Calabi-Yau é um molde potencial para um Cosmos inteiramente novo, com um conjunto de vibrações (e, portanto, de partículas) diferentes.
O problema é que, na hipótese mais otimista, o número de formas de Calabi-Yau que são candidatas viáveis a gerar um Universo como o nosso está na casa das dezenas de milhares, e ninguém ainda sabe como deduzir, a partir das equações, qual é a forma certa. “O esquema matemático da teoria de cordas é tão complexo que os físicos só foram capazes de efetuar cálculos aproximados graças a uma formalização denominada teoria da perturbação”, escreve Greene.
Outro problema da teoria de cordas é que, para funcionar, ela exige um novo tipo de simetria. É um termo cabeludo de explicar, então vamos nos ater à sua consequência prática: para cumprir essa exigência, cada partícula do Modelo Padrão precisaria ter uma partícula irmã equivalente; uma espécie de espelho. E não há qualquer evidência de que o Universo tenha vindo de fábrica com esse pacotão extra de tijolinhos fundamentais, ainda que essa seja uma possibilidade tentadora, por vários motivos. Por isso, os teóricos de cordas supõem que essas partículas sejam extremamente pesadas, e que para observá-las precisamos (como no caso anterior) de experimentos com energias muito mais altas do que as alcançadas hoje no LHC.
Essa simetria, chamada supersimetria, ainda não dá conta do recado sozinha. Para adequar novamente a teoria de cordas ao comportamento das partículas no mundo real, foi necessário incluir mais um ingrediente, chamado paridade-R. Outro problema é que a teoria de cordas parece funcionar melhor em um Universo com constante cosmológica negativa, mas observações realizadas em 1998 mostraram que a constante é positiva, porque o Universo está se expandindo de forma acelerada. (Essa não é, evidentemente, uma lista exaustiva das dificuldades da teoria de cordas, mas apenas um breve resumo, muito simplificado.)
O debate
O físico George Matsas, pesquisador do Instituto de Física Teórica da Unesp, em São Paulo, explica à RQC que a unificação final da física é uma meta ambiciosa como já foi alcançar a Lua. Os teóricos de cordas tentam abordá-la construindo uma Torre de Babel, porque uma solução mais direta, como um foguete, ainda não está ao alcance dos métodos atuais. Daí nasce uma sequência de ajustes e adições (como compactar as dimensões extras para evitar o problema de que só observamos quatro delas), que visam manter a teoria de cordas adequada ao que já sabemos sobre a natureza, porém sem aproximá-la da verificação na prática.
Críticos como Peter Woit e Lee Smolin, já mencionados no texto, ou Sabine Hossenfelder (autora de outro livro que critica o estado da física contemporânea, intitulado Lost in Math, em português, “Perdidos na matemática”) movimentam um debate público ativo em torno da teoria de cordas, que se espalha por posts de blog pouco amistosos, entrevistas cheias de argumentos ad hominem e vídeos no YouTube. Existem até sites dedicados a compilar as principais referências bibliográficas da briga, como este ou este. Essas críticas mudaram o tom das discussões sobre a teoria, que havia entrado no novo milênio vista de maneira majoritariamente positiva (não só no meio acadêmico como na imprensa e nas prateleiras de divulgação científica).
Um ponto central desses debates é que os céticos criticam a tendência dos teóricos de cordas de usar a beleza subjetiva da matemática como uma luz para guiá-los na vanguarda da física. Equações sucintas com grande poder explicativo geram nos físicos mais idealistas a intuição de que eles estão farejando um caminho promissor.
Isso é compreensível. A teoria de cordas nasceu em resposta à necessidade intelectual de unir duas teorias muito poderosas, mas incompatíveis. Nesse aspecto, ela é diferente da mecânica quântica, que foi uma reação a um problema pé no chão: explicar por que observações realizadas em laboratório no século 19 (especificamente, o efeito fotoelétrico e a radiação de corpo negro) davam resultados que não correspondiam aos previstos pela física clássica.

Essa maneira abstrata como a teoria de cordas veio ao mundo não foi uma opção, mas uma necessidade: embora o Modelo Padrão tenha suas falhas explicativas, ele ainda prevê os resultados de todos os experimentos com precisão altíssima. Não há buracos evidentes por onde se possa começar a destrinchá-lo em busca do próximo passo, como houve em outras ocasiões na história da Física. Daí a confiança na matemática. De fato, o filósofo da ciência Richard Dawid da Universidade de Estocolmo escreveu um livro inteiro (String theory and the scientific method, “Teoria de cordas e o método científico”) argumentando que, na paisagem atual da Física, a verificação pela via experimental não pode ser a única régua possível para o método científico.
O problema é: por que a natureza haveria de obedecer aos critérios estéticos subjetivos de uma espécie de primatas particularmente inteligentes evoluída no leste da África? O próprio Brian Greene, que fez uma sólida carreira explicando teoria de cordas para o público amplo em best sellers de divulgação científica, admite que os físicos teóricos se dividem entre os que preferem se manter na rabeira dos experimentos, trabalhando sempre com base em evidências, e os que preferem usar a matemática para especular sobre aspectos da natureza que ainda estão fora do nosso alcance – mesmo que não haja qualquer esperança de investigá-los na prática tão cedo. É uma diferença de postura filosófica que vai além dos números.
A defesa
As respostas dos teóricos de cordas às objeções acima tomam diferentes caminhos, que explicaremos resumidamente abaixo. O primeiro é a falta de opção melhor: por mais que a teoria ainda não forneça possibilidades de verificação empírica, ela representa a linha de investigação mais frutífera disponível para quem quer encarar o problema da unificação entre mecânica quântica e relatividade geral (outras opções, como a chamada loop quantum gravity, são ainda mais polêmicas). Existem excelentes motivos para acreditar, por exemplo, que há uma forma de Calabi-Yau capaz de gerar os resultados teóricos adequados ao nosso Universo, mesmo que a matemática ainda não nos permita alcançá-la.
Nas palavras do Prêmio Nobel Sheldon Glashow, crítico da área, ainda nos anos 1980: “Nós, os teóricos que não aderiram à teoria de cordas, não fizemos nenhum progresso na última década. (...) Existem problemas que não encontram resposta da teoria quântica de campo convencional (...) E o único outro esquema que eu conheço é a teoria de cordas.”
O segundo é que pensar no mundo microscópico em termos de cordas não serve apenas para tentar a grande unificação. De fato, além das duas últimas décadas terem sido marcadas por uma redução clara no número de pesquisadores que se dedicam às cordas e no número de papers publicados sobre o assunto, a maioria dos teóricos de cordas, hoje, busca aplicar seus conhecimentos a outros problemas, mais acessíveis e com potencial de sucesso verificável em curto prazo.
Um terceiro ponto é argumentar que, na verdade, a teoria de cordas é sim verificável. O problema é que suas previsões até agora já são conhecidas, o que as tornariam mais próximas de “pós-visões”. Edward Witten, talvez o nome mais conhecido das cordas, argumenta que a existência de um padrão vibratório correspondente ao gráviton dentro da teoria é, por si só, uma evidência a seu favor. A ideia é que, se uma civilização fictícia por qualquer motivo descobrisse a teoria de cordas antes da gravitação de Newton, essa civilização seria capaz de deduzir o funcionamento da gravidade a partir dela.
Outra divergência entre os defensores e críticos da teoria de cordas gira em torno da possibilidade de pesquisadores frustrados com as cordas mudarem suas linhas de pesquisa após uma certa etapa na carreira. Para os mais céticos, o fato de que muitos físicos ainda abraçam a teoria tem uma explicação prática: é difícil se tornar um especialista nesse assunto, e mais difícil ainda trocar de especialidade no meio da carreira. Para quem começou a estudar cordas na juventude, uma guinada tão tardia simplesmente não é cômoda (ou sequer viável).
As cordas podem até não ser a tão buscada “Teoria de Tudo”, mas isso não significa que os avanços radicais que elas trouxeram, especialmente na arena da matemática, não possam servir de trampolim para capítulos mais promissores no futuro. Leonard Susskind, pai da teoria de cordas, diz: “(...) Essa coisa supersimétrica e matematicamente precisa não descreve o mundo em que vivemos. (...) O que nós sabemos é que a teoria de cordas tem uma estrutura precisa que inclui mecânica quântica e gravidade, e que é consistente. Isso é algo grande. Como podemos torná-la uma teoria sobre a realidade? Eu não sei”.
“A teoria de cordas ficou na defensiva nas relações públicas, mesmo que a maioria dos teóricos repudiem as alegações de Woit ou Smolin como tentativas falhas de desacreditá-la em benefício próprio”, resume o teórico de cordas Daniel Robbins, da Universidade Texas A&M. “A verdade provavelmente está em algum ponto no meio do caminho: as críticas têm mais valor do que os teóricos de cordas tendem a dar, mas não são tão destrutivas quanto Woit, principalmente, faz seus leitores acreditarem”.
No fundo, todos os físicos – dos mais durões aos que se deixam levar pela beleza dos números – buscam a mesma coisa: uma pista para dar o próximo passo na nossa compreensão do Cosmos. Conforme os cientistas se debruçam sobre distâncias cada vez menores, os experimentos disponíveis se tornam cada vez menos capazes de guiá-los. A questão é: será que a elegância e a intuição matemática podem preencher essa lacuna, ou a ideia de que a natureza obedece a nossas expectativas estéticas nos levará por caminhos infrutíferos? Só o tempo (ou um acelerador de partículas do tamanho do Universo) nos dirá.
Bruno Vaiano é jornalista
