
E daí?[i] Com capacidade para até 850 passageiros, o Airbus A380 é o maior avião comercial do mundo[ii]. Considerando os dados oficiais do Ministério da Saúde, entre 17/5 e 23/5, o Brasil perdeu 6.380 vidas para COVID-19, o que significa uma média diária de 911 óbitos. É como se todo dia um avião lotado desse porte caísse durante uma semana seguida (ver Tabela 1).
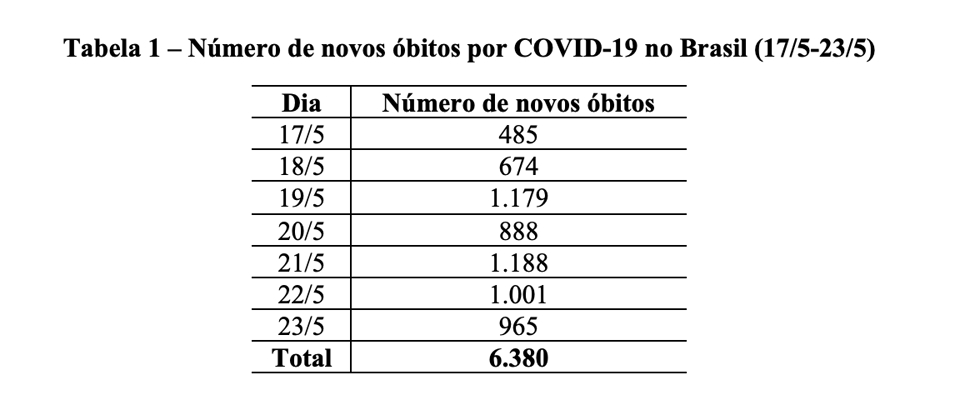
Comparativamente, a gravidade do problema já colocou o Brasil no triste grupo de países com mais de 20 mil óbitos. Considerando os dados de 24/5, às 8h22, os Estados Unidos lideram o ranking de mortalidade com 98.683 ocorrências fatais. O Reino Unido, que durante algum tempo apostou em estratégias menos restritivas de controle social, contabiliza 36.675 óbitos. A Itália totaliza 32.735 baixas. Espanha (28.678) e França (28.332) brigam pela quarta posição no ranking absoluto de vidas perdidas. O Brasil aparece na sexta colocação com 22.165 óbitos[iii] (ver Tabela 2).
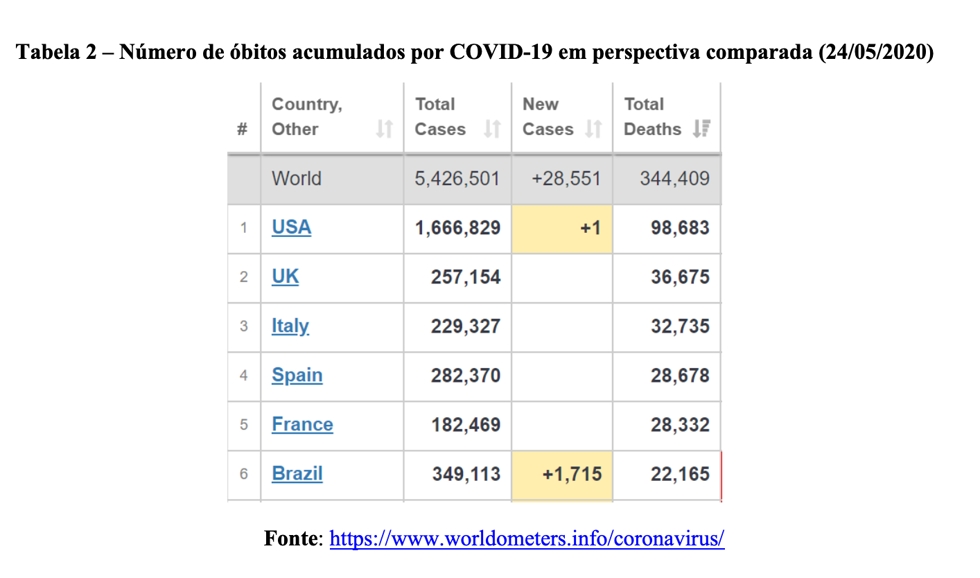
Para melhor compreender a dinâmica longitudinal dos dados, a Figura 1 ilustra variação do número acumulado de óbitos nos Estados Unidos e no Reino Unido.
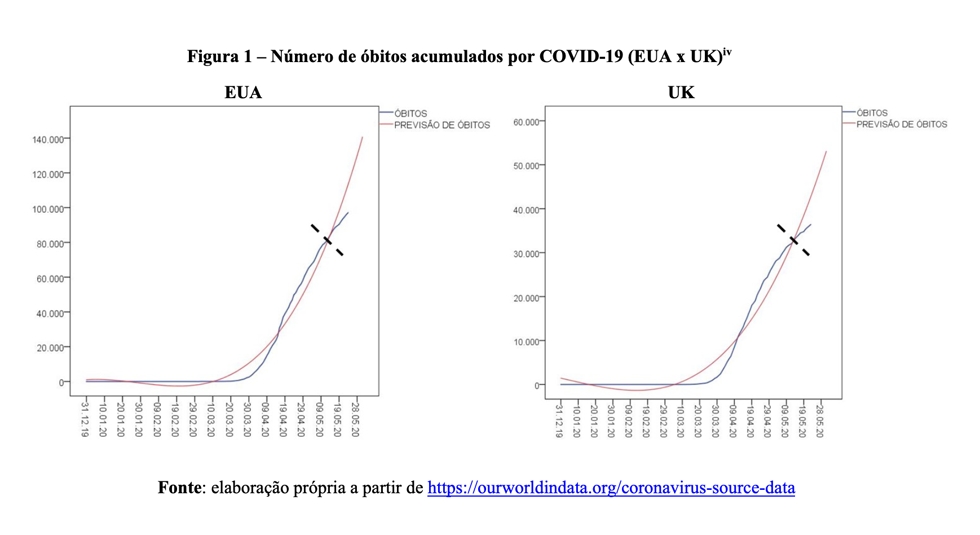
Vejamos como interpretar: a linha azul representa a quantidade observada de óbitos. Por sua vez, a linha vermelha ilustra a previsão do número de mortes a partir de um modelo matemático extremamente pessimista e apocalíptico[iv]. Quando a curva azul está mais alta do que a curva vermelha, isso é sinal de que nosso modelo está subestimando o real valor da variável de interesse. Contrariamente, quando a curva vermelha está mais alta do que a linha azul, isso significa que nossa previsão superestima a quantidade de mortes. Finalmente, quando as curvas se tocam, temos a situação em que o valor da previsão é exatamente igual ao valor observado.
Note que há momentos que o modelo superestima o verdadeiro número de óbitos (curva vermelha acima da curva azul). Mas também há dias em que ocorre o contrário, a curva azul é mais alta do que a vermelha, o que indica que nosso modelo foi mais otimista do que a realidade. A tendência é tão parecida em ambos os países que mais parece que estamos olhando para gráficos duplicados. O importante, no entanto, é quando as curvas parecem tomar rumos distintos (linha pontilhada preta). Isso significa que o modelo é incapaz de prever o comportamento da série de dados. E isso acontece por um motivo simples: a quantidade de novos óbitos está desacelerando. Assim, é seguro inferir que, daqui em diante, a curva vermelha vai indicar previsões extremamente distantes do verdadeiro valor de mortes. Vejamos a situação da Itália e da Espanha (Figura 2).
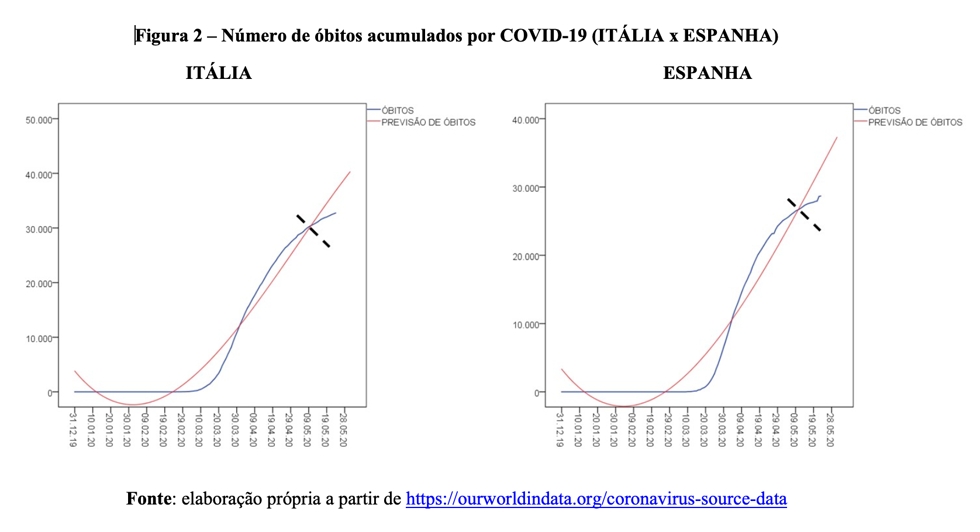
Similarmente ao que vimos nos Estados Unidos e no Reino Unido, a curva de mortalidade (azul) parece estar tomando outro caminho, bastante distinto daquele perseguido pela curva vermelha de crescimento acelerado. Ou seja, Itália e Espanha estão experimentando uma redução na quantidade diária de novas mortes, o que por sua vez reduz o ritmo de incremento dos óbitos acumulados ao longo do tempo. Dessa forma, também é seguro inferir que, pelo menos para a primeira onda de infecções, a curva vermelha vai gerar previsões estapafúrdias. Vejamos a situação da França e do Brasil (Figura 3).
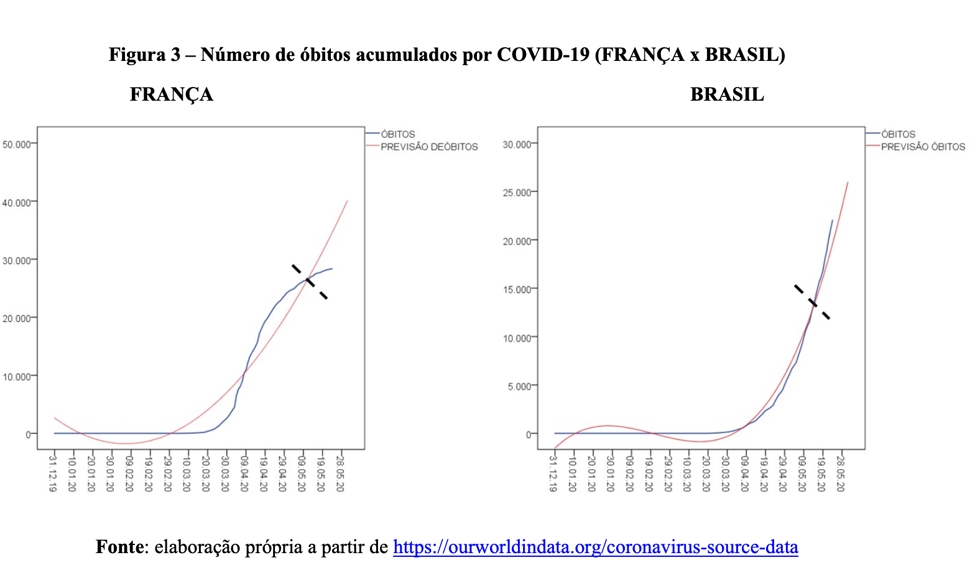
Note que a França reproduz o mesmo padrão observado nos Estados Unidos, Reino Unido, Itália e Espanha, qual seja: depois da última interseção entre as curvas (ver linha pontilhada preta), os valores observados são menores do que os valores previstos pelo modelo. No Brasil, por outro lado, a curva azul está sistematicamente à frente da curva vermelha. Ou seja, o modelo tende a subestimar o verdadeiro valor dos óbitos em nosso país. Para melhor visualizar essa tendência, vejamos a Figura 4, que ilustra a distribuição do erro de previsão do modelo em perspectiva comparada.
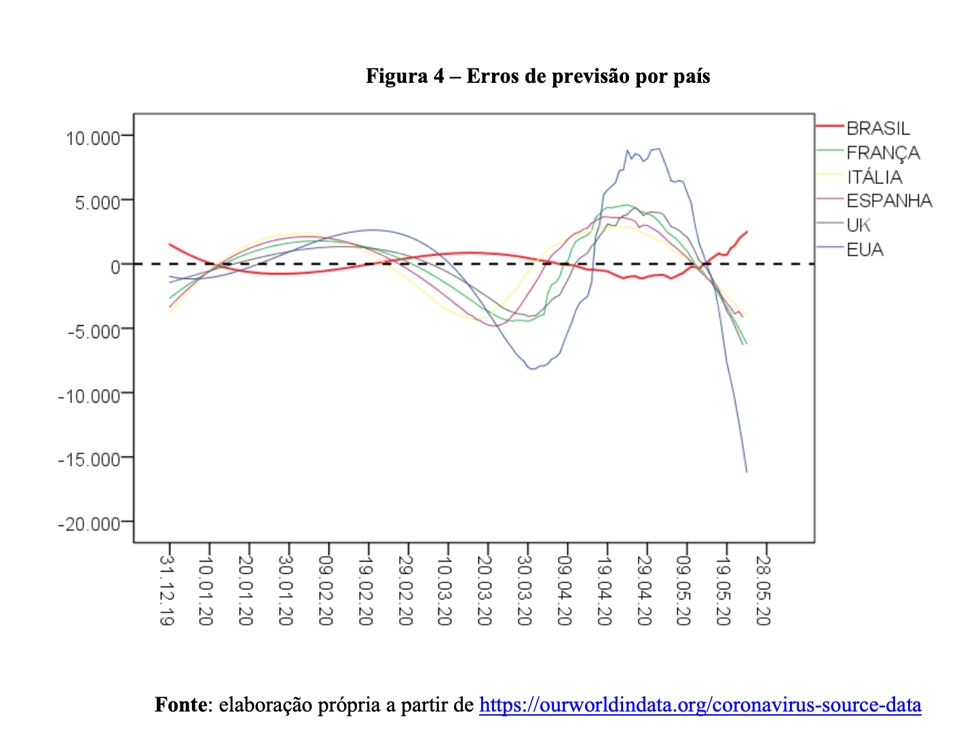
Em estatística, um dos pressupostos de um modelo bem ajustado é que o erro tenha média zero (ver linha pontilhada preta na Figura 4). Isso significa que nossa estimativa não tende a subestimar, nem a superestimar o verdadeiro valor do parâmetro de interesse. Como pode ser observado pelo comportamento da curva vermelha, somos o único país analisado em que o total de mortes é maior do que o previsto pelo modelo (lembrando que dissemos que nossa previsão era extremamente pessimista e apocalíptica).
Em particular, a estimativa pontual para o dia 31/05/2020 é de 25.944 óbitos. Mas nós já sabemos que esse modelo é incapaz de descrever adequadamente a trajetória dos dados uma vez que se morre muito mais rápido do que a linha vermelha é capaz antever. De acordo com nossos cálculos, devemos observar a queda de pelo menos oito aviões Airbus A380 no país até o próximo domingo, totalizando mais de 7.000 novos óbitos. Com as 22 mil mortes já registradas, o Brasil deve ultrapassar a marca de 30 mil vidas perdidas e desbancar França e Espanha nos próximos dez dias.
E o pior de tudo é saber que são mortes evitáveis. Daí a dificuldade de entender a obsessão de alguns gestores governamentais em ignorar a adoção de políticas públicas baseadas em evidências.
Dalson Britto Figueiredo Filho é professor-assistente de Ciência Política na Universidade Federal de Pernambuco (UFPE)
Antônio Fernandes é mestrando em Ciência Política na Universidade Federal de Pernambuco (UFPE)
Lucas Silva é cientista político e estudante de Medicina na Universidade Estadual de Ciências da Saúde de Alagoas
Enivaldo Rocha tem graduação em Estatística (UFPE), mestrado em Estatística (USP) e doutorado em Engenharia de Produção (UFRJ). É professor titular aposentado da Universidade Federal de Pernambuco e membro do Grupo de Métodos em Pesquisa em Ciência Política (MPCP)
NOTAS
[i] Tradução do título da música So What, que serviu de inspiração para este artigo, ver: < https://www.youtube.com/watch?v=0XoyDqFy5pU >.
[ii] https://economia.uol.com.br/todos-a-bordo/2020/01/23/maiores-avioes-comerciais.htm
[iii] O portal do Ministério da Saúde informa 22.013 mortes até 23/05/2020.
[iv] Tecnicamente, utilizamos um modelo de regressão polinomial com grau 3º. Os dados estão disponíveis em: < https://ourworldindata.org/coronavirus-source-data >. Para aplicações dessa perspectiva, ver Pandey et al (2020) e Gupta e Pal (2020).
Notas do Conselho Editorial
Alguns profissionais que trabalham com modelagem matemática levantaram críticas ao artigo acima. O professor Marcelo Yamashita, diretor do Instituto de Física Teórica (IFT) da Unesp e membro do Conselho Editorial da Revista Questão de Ciência, encaminhou à redação as considerações abaixo:
O artigo "COVID-19 no Brasil: um avião de passageiros caindo por dia, todo dia" faz uma análise do número de óbitos no Brasil por conta da pandemia de COVID-19. Em termos do tratamento dos dados, gostaria de apontar as seguintes ressalvas:
Não dá para entender o que significa a curva azul e a vermelha na Fig. 1. Se a curva azul representa os óbitos (dados discretos), então não faz sentido ser uma linha, tem que aparecer os pontos. A curva vermelha não representa uma "previsão", mas é apenas um ajuste de curva. Uma previsão, proveniente de um modelo epidemiológico - SIR, por exemplo - deve contemplar as nuances da doenças e outros aspectos populacionais. O atual ajuste, um polinômio de terceiro grau, tem uma janela limitada de aplicabilidade. Não dá, a priori, para saber até onde funcionará.
Não é possível afirmar o que está no trecho seguinte: "O importante, no entanto, é quando as curvas parecem tomar rumos distintos (linha pontilhada preta). Isso significa que o modelo é incapaz de prever o comportamento da série de dados. E isso acontece por um motivo simples: a quantidade de novos óbitos está desacelerando. Assim, é seguro inferir que, daqui em diante, a curva vermelha vai indicar previsões extremamente distantes do verdadeiro valor de mortes".
A mudança da derivada do polinômio de terceiro grau acontece de maneira fortuita, já que o ajuste foi feito considerando apenas o período contemplado na figura. Provavelmente, um polinômio do terceiro grau não é a melhor curva para prever pontos de uma pandemia. Para ver isso é só considerar que esse polinômio vai crescer ou decrescer indefinidamente. Para tempos bem curtos isso pode funcionar (para tempos curtíssimos, até uma reta funciona).
O mesmo comentário vale para as figuras 2 e 3 e os parágrafos colocados logo em seguida.
A seguinte afirmação está errada: “Em estatística, um dos pressupostos de um modelo bem ajustado é que o erro tenha média zero (ver linha pontilhada preta na Figura 4)”. Uma maneira simples de ver isso é que você poderia colocar um polinômio de grau elevado que oscilaria loucamente, mas passaria exatamente pelos pontos. Isso, porém, não seria um modelo bem ajustado simplesmente por não corresponder à realidade. O que se deve verificar não é a média, mas a soma dos quadrados das diferenças, ponderada pelas incertezas e considerando os graus de liberdade no ajuste - tudo isso levando-se em conta o critério de verossimilhança da curva utilizada.
Fazer uma estimativa cravando um número com precisão de unidade é ruim. Ainda mais utilizando um ajuste cuja extrapolação é duvidosa.
Resposta aos comentários ao artigo “COVID-19 no Brasil: um avião de passageiros caindo por dia, todo dia”.
É muito gratificante receber comentários ao artigo “COVID-19 no Brasil: um avião de passageiros caindo por dia, todo dia”. Acreditamos fortemente que a produção científica avança a partir do debate qualificado entre os pares. E, por isso, agradecemos as críticas. Todavia, o conteúdo dos questionamentos deixa claro que alguns pontos podem ser melhor explicados. O principal objetivo deste artigo é dirimir eventuais dúvidas sobre as técnicas utilizadas e as inferências apresentadas no trabalho original. Metodologicamente, examinamos informações secundárias do Ministério da Saúde e do European Centre for Disease Prevention and Control (ECDC). Para facilitar a leitura, organizamos este documento em função das críticas recebidas e das respectivas respostas.
CRÍTICA 1
Não dá para entender o que significa a curva azul e a vermelha na Fig. 1. Se a curva azul representa os óbitos (dados discretos), então não faz sentido ser uma linha, tem que aparecer os pontos. A curva vermelha não representa uma "previsão", mas é apenas um ajuste de curva. Uma previsão, proveniente de um modelo epidemiológico - SIR, por exemplo - deve contemplar as nuances da doenças e outros aspectos populacionais. O atual ajuste, um polinômio de terceiro grau, tem uma janela limitada de aplicabilidade. Não dá, a priori, para saber até onde funcionará.
Resposta:
A curva azul, como indicado no artigo original, indica a quantidade de óbitos acumulados. Em termos de nível de mensuração, a contagem de mortes é, como corretamente indica a crítica, uma variável discreta, tal qual o número de gols em uma partida de futebol ou a votação de um candidato durante as eleições. Discordamos, todavia, da posição de que dados discretos não podem ser representados por linhas. O Worldmeters, por exemplo, representa a variação da mortalidade em função do tempo com gráficos de linhas (ver). Similarmente, as análises estatísticas do Departamento de Medicina da Universidade Johns Hopkins também emprega gráficos de linha com essa finalidade (ver). Com efeito, o livro do George Box e colaboradores (ver), uma das obras mais importantes da área de séries temporais, utiliza gráfico de linhas para ilustrar a variação de séries discretas (ver, por exemplo, o capítulo 6 sobre identificação do modelo). Mais recentemente, os professores Rob Hyndman e George Athanasopoulos publicaram um livro que ensina a fazer previsões com auxílio do pacote R (ver). A Figura 1, reproduzida abaixo, ilustra a variação da quantidade de passageiros de avião na Austrália.
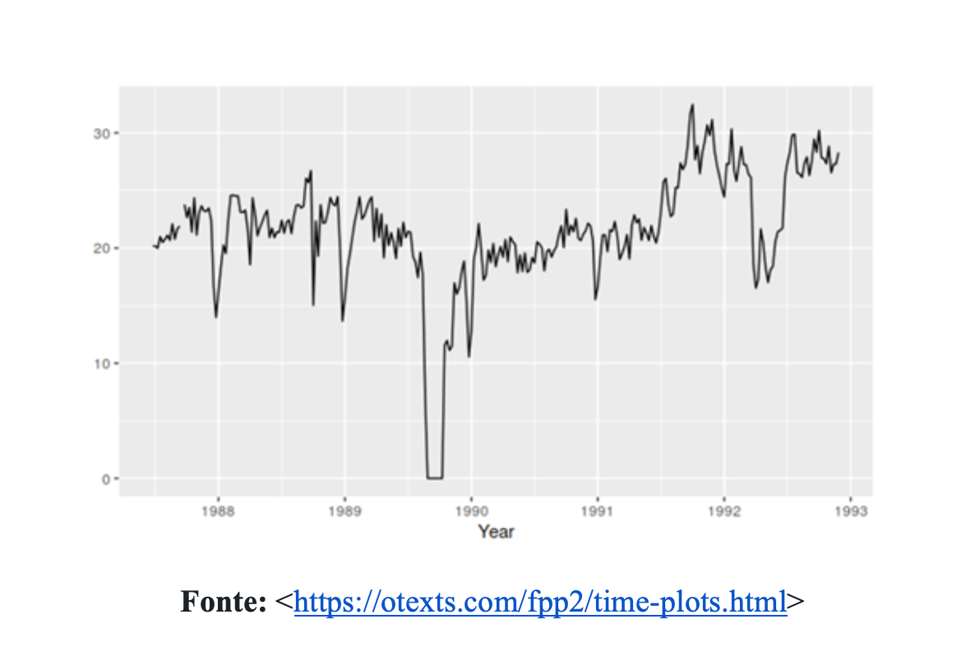
Outro exemplo famoso de uma série de dados discreta que é usualmente examinada com gráfico de linha é a variação mensal do número de passageiros de avião nos Estados Unidos entre 1949 e 1960 (ver Figura 2).
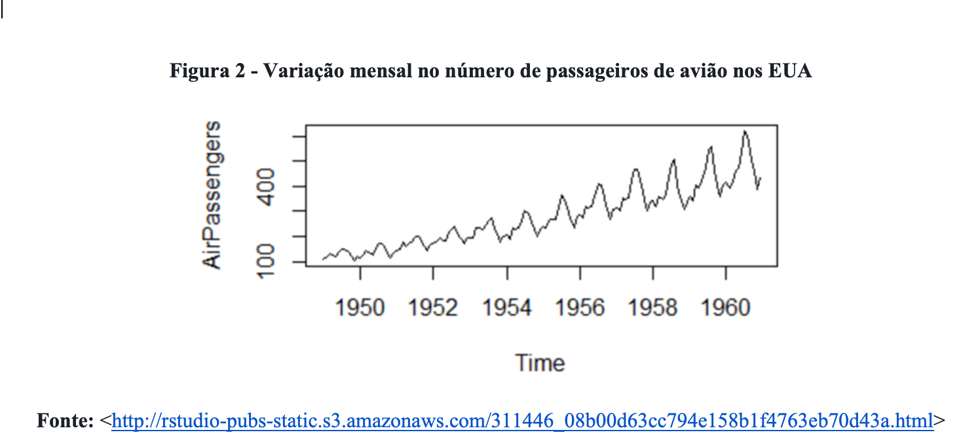
Acreditamos que, para esse caso em particular, a escolha entre usar linha ou pontos é meramente estilística e não afeta substantivamente as inferências. Vejamos, por exemplo, a variação da quantidade acumulada de óbitos por COVID-19 no Brasil em função do tempo. A Figura 3 ilustra essas informações.
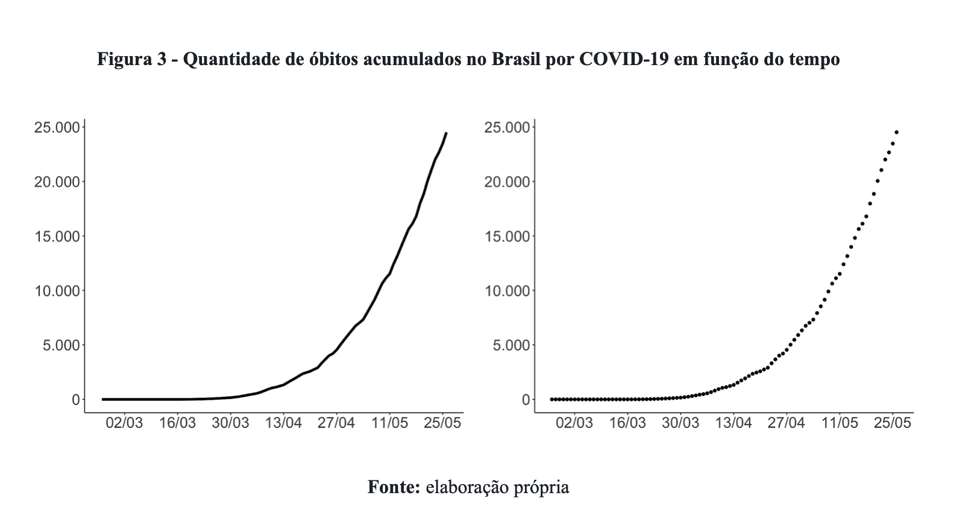
Não há perda de informação. A conclusão que chegaríamos a partir da análise do gráfico com pontos é exatamente igual à inferência realizada a partir do exame do gráfico com linhas. Por fim, considerando que um dos objetivos da Revista Questão de Ciência é promover a divulgação científica para um público amplo, entendemos que o gráfico de linha é mais popular do que o gráfico de pontos.
No que diz respeito ao significado da curva vermelha, como também indicado no texto original, ela ilustra “a previsão do número de mortes a partir de um modelo matemático extremamente pessimista e apocalíptico”. Como se trata de um artigo de divulgação científica, tentamos reduzir a complexidade matemática do modelo com o objetivo de facilitar a compreensão do argumento. Todavia, como ficou evidente pela natureza da crítica 1, parece que isso não funcionou. Talvez agora seja o momento de explicar melhor o passo a passo do que fizemos.
Existem várias estratégias que podem ser empregadas para gerar modelos de previsão. A adequabilidade das diferentes técnicas depende, entre outras coisas, do tipo de dados disponível. Os modelos SIR, por exemplo, consideram uma série de parâmetros para modelar a propagação da epidemia em função do tempo (ver). Em séries temporais, por sua vez, podemos tentar identificar algum padrão no conjunto dos dados e assumir que esse padrão se manterá constante no futuro. Em regressão, por outro lado, podemos prever o valor esperado de uma variável dependente, digamos peso, em função de uma ou mais variáveis independentes, digamos altura e idade. Quanto mais bem ajustado o modelo, menores serão os erros de previsão. Em nosso artigo original, adotamos um modelo de regressão polinomial para descrever a variação do número acumulado de óbitos em função do tempo. Observe que não estamos diante de um modelo explicativo, em que X exerce um efeito causal sobre Y. Estamos cientes de que o ajuste cúbico implica em um crescimento indefinido da curva, mas exatamente por isso utilizamos os qualificadores “extremamente pessimista e apocalíptico”. Assim, enquanto a curva de óbitos estiver crescendo em ritmo acelerado, julgamos adequada a utilização da regressão polinomial como ferramenta de previsão do número acumulado de óbitos por COVID-19 no Brasil. Vejamos, por exemplo, qual é a capacidade preditiva do nosso modelo.
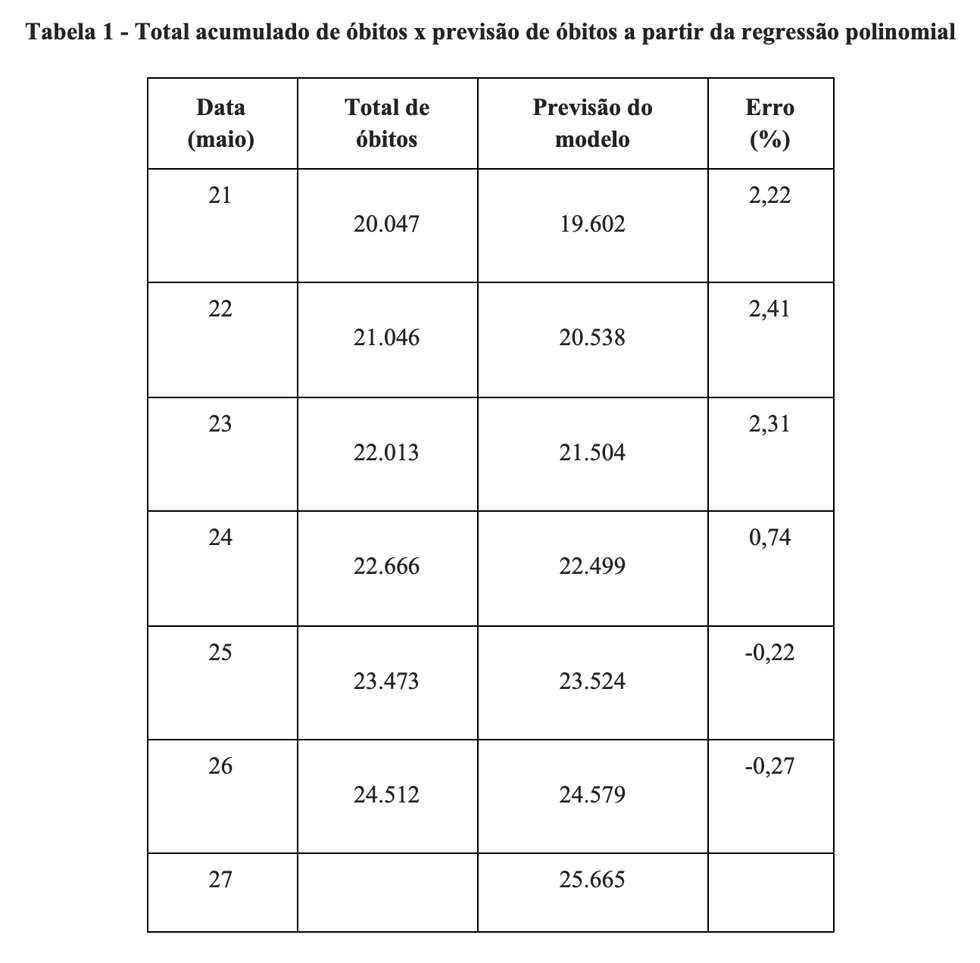
A Tabela 1 tem quatro variáveis de interesse: 1) data; 2) número de óbitos acumulados (observado); 3) previsão da quantidade de óbitos realizada a partir do modelo de regressão polinomial e 4) erro percentual, calculado a partir da diferença entre os valores observados e os previstos. Entre 21 e 24 de maio de 2020, o modelo subestimou ligeiramente o valor do parâmetro. Ou seja, nossa previsão foi menor do que o valor verdadeiramente registrado de óbitos por COVID-19. Entre 25 e 26, o modelo começa a superestimar o valor do parâmetro, ou seja, o valor previsto de óbitos foi maior do que a verdadeira quantidade de mortes contabilizadas no Brasil.
Em média, isso quer dizer que nosso modelo errou 1,20% (média aritmética das diferenças percentuais). Em particular, para o último dia disponível, o erro foi de apenas 67 óbitos, o que significa uma diferença percentual residual de apenas 0,27% em relação à realidade. Assim, discordamos da afirmação de que não temos uma previsão. Temos sim. Nosso modelo pode não ser tão sofisticado como os modelos epidemiológicos, mas não resta dúvida de que tem acurácia preditiva, principalmente no curto prazo (até 10 dias no futuro).
E até quando poderemos utilizar um polinômio de terceiro grau para descrever a mortalidade por COVID-19 no Brasil? Não sabemos. Todavia, a análise diária dos dados, incluindo a análise gráfica da série e o exame cuidado dos resíduos certamente indicará o momento em que esse modelo começar a se tornar obsoleto. Essa foi exatamente a nossa intenção ao mostrar graficamente a variação dos resíduos em perspectiva comparada. Vejamos novamente a Figura 4.
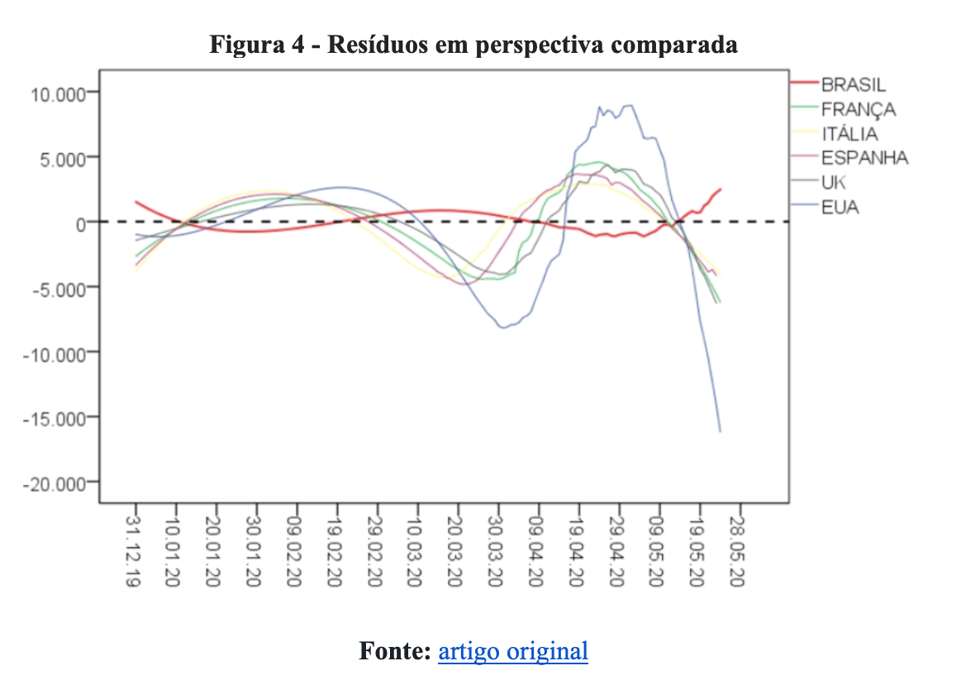
Não resta dúvida de que o modelo polinomial é incapaz de descrever adequadamente o comportamento da mortalidade por COVID-19. O exame dos valores mais recentes indica isso: o modelo superestima sistematicamente o real valor do parâmetro de interesse para a maior parte dos países. A única exceção é o Brasil uma vez que a curva vermelha está na área positiva do gráfico. A nossa conclusão então foi afirmar que a mortalidade no país cresce muito mais rápido do que um polinômio de terceiro grau é capaz de prever. O título do artigo original informou que teríamos um avião de passageiros caindo por dia, todo dia. Vejamos o que diz a realidade. Em 24/5, foram computados 653 óbitos. No dia 25 foram 807 óbitos e ontem perdemos 1.039 vidas. Em média, isso significa 833 almas consumidas, lembrando que a capacidade do Airbus A380 é de 850 passageiros.
CRÍTICA 2
Não é possível afirmar o que está no trecho seguinte: “O importante, no entanto, é quando as curvas parecem tomar rumos distintos (linha pontilhada preta). Isso significa que o modelo é incapaz de prever o comportamento da série de dados. E isso acontece por um motivo simples: a quantidade de novos óbitos está desacelerando. Assim, é seguro inferir que, daqui em diante, a curva vermelha vai indicar previsões extremamente distantes do verdadeiro valor de mortes”.
Resposta:
O comportamento do vírus no Brasil apresenta várias nuances que dificultam a previsão acurada da realidade epidemiológica. Até os modelos mais complexos não conseguem incorporar adequadamente questões importantes que influenciam a dinâmica da infecção, como a variação da densidade populacional domiciliar nos grandes centros urbanos, por exemplo. Esse tipo de limitação também está presente no modelo elaborado, indicando que não é possível obter uma previsão com alto grau de validade diante desse cenário. Quanto maior o horizonte temporal da previsão, maior o nível de incerteza. Isso é verdadeiro para qualquer modelagem estatística.
Acreditamos que o nosso modelo busca apresentar de maneira didática a evolução da mortalidade e ilustrar alguns possíveis desdobramentos no curto prazo. Artigos recentes, como Pandey et al (2020), mostram resultados semelhantes de estimativas calculadas a partir de modelos SEIR e de regressão na identificação do número de casos de COVID-19. O problema para identificação no número de óbitos é apresentado pelos autores da seguinte forma:
In this study, we have only predicted the number of confirmed cases. To predict the number of death cases we faced many problems of data stationarity. Also, with limited data, the model was not able to predict the number of death cases properly. We have used only time series data for confirmed cases and death cases in this study. Using other data related to weather, geographic layout of the country, state-level population and governance parameters, the model prediction rate can be further improved (PANDEY et al 2020, p. 8).
A Figura 5 foi retirada das previsões de Pandey et al (2020) que compara as estimativas de um modelo SEIR x modelo regressão polinomial.
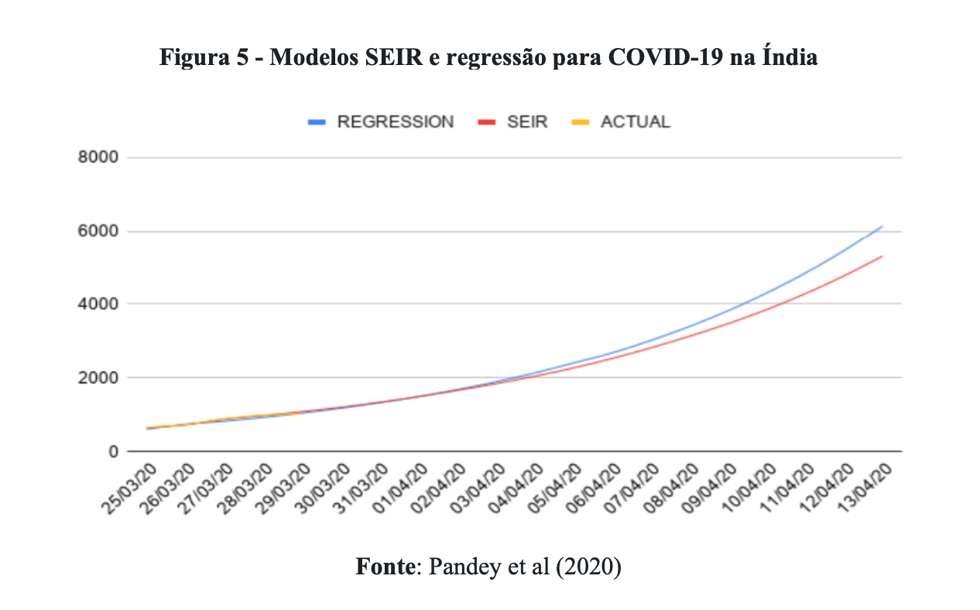
Observe que os valores estimados são parecidos, mas o modelo de regressão cresce em um ritmo ligeiramente mais acelerado. De acordo com as estimativas do European Centre for Disease Prevention and Control (ECDC), a Índia registrou 9.152 casos no dia 13/04/2020. Assim, ambos os modelos subestimaram o verdadeiro valor de interesse, mas o modelo de regressão errou um pouco menos.
À exceção do Brasil, todos os países mais afetados já exibem desaceleração na quantidade de novos óbitos. Por isso, ratificamos nossa posição do artigo original de que a utilização de um modelo polinomial “vai indicar previsões extremamente distantes do verdadeiro valor de mortes”. A Figura 6 apresenta a quantidade de mortes diárias confirmadas de covid-19 no Brasil, Estados Unidos, Reino Unido, Espanha, Itália e França.
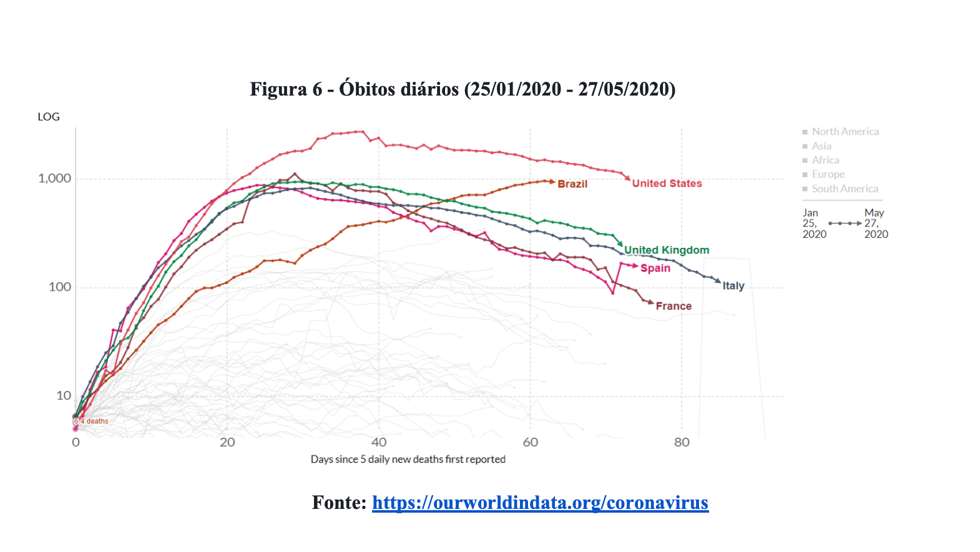
Tecnicamente, o efeito da redução de novos óbitos é a formação de um platô na curva de óbitos acumulados, conforme ilustra a Figura 7.
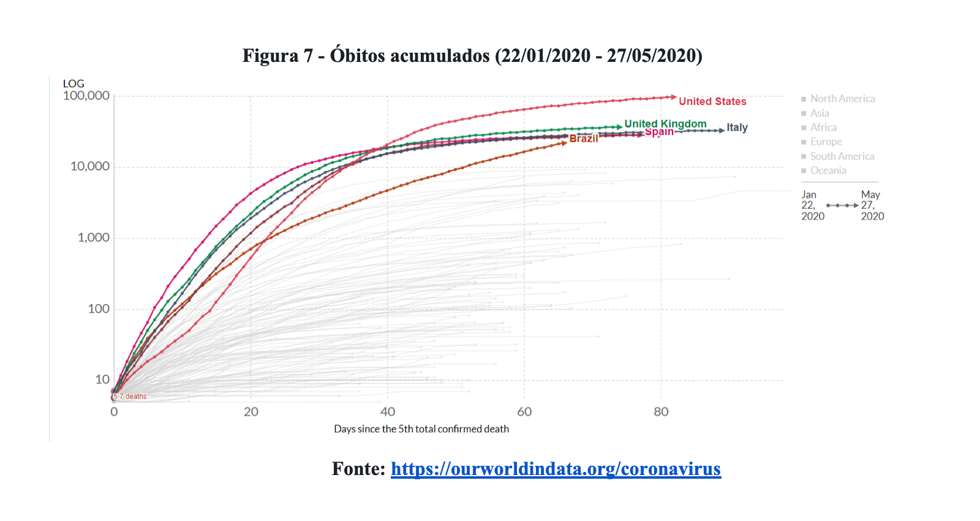
Comparativamente, considerando os dados mais recentes, o Brasil é o único país da amostra examinada que exibe tendência positiva. Assim, diante do exposto, consideramos válida a inferência de que o Brasil segue um caminho muito diferente daquele trilhado por Estados Unidos, Reino Unido, Itália, Espanha e França.
CRÍTICA 3
A mudança da derivada do polinômio de terceiro grau acontece de maneira fortuita, já que o ajuste foi feito considerando apenas o período contemplado na figura. Provavelmente, um polinômio do terceiro grau não é a melhor curva para prever pontos de uma pandemia. Para ver isso é só considerar que esse polinômio vai crescer ou decrescer indefinidamente. Para tempos bem curtos isso pode funcionar (para tempos curtíssimos, até uma reta funciona).
Resposta:
De fato, um polinômio do terceiro grau não é a melhor curva para prever pontos de uma pandemia. Assim como a curva exponencial também não é. Na verdade, tanto o modelo cúbico quanto a curva exponencial tendem a crescer ou decrescer indefinidamente, como bem colocou nosso comentarista.
Como estamos diante de uma população finita (número de pessoas vivendo no Brasil), é impossível qualquer curva de infecção crescer para sempre. Em algum momento, veremos uma desaceleração e, em seguida, a formação de um platô. De nenhuma forma sugerimos que o modelo estimado a partir de um polinômio do terceiro grau é capaz de produzir previsões confiáveis de longo prazo. Se isso não ficou suficientemente explícito no artigo original, esse é o momento de apontar que essa perspectiva funciona apenas para intervalos curtos de tempo. Mas curtos quanto? Não tem como saber. Para o Brasil, por exemplo, a adoção de um polinômio do terceiro grau parece se ajustar bem aos dados disponíveis até 27/05/2020. Por exemplo, vejamos a distribuição da quantidade prevista de óbitos e o número observado de mortes no Brasil de acordo com o nosso modelo (Figura 8).
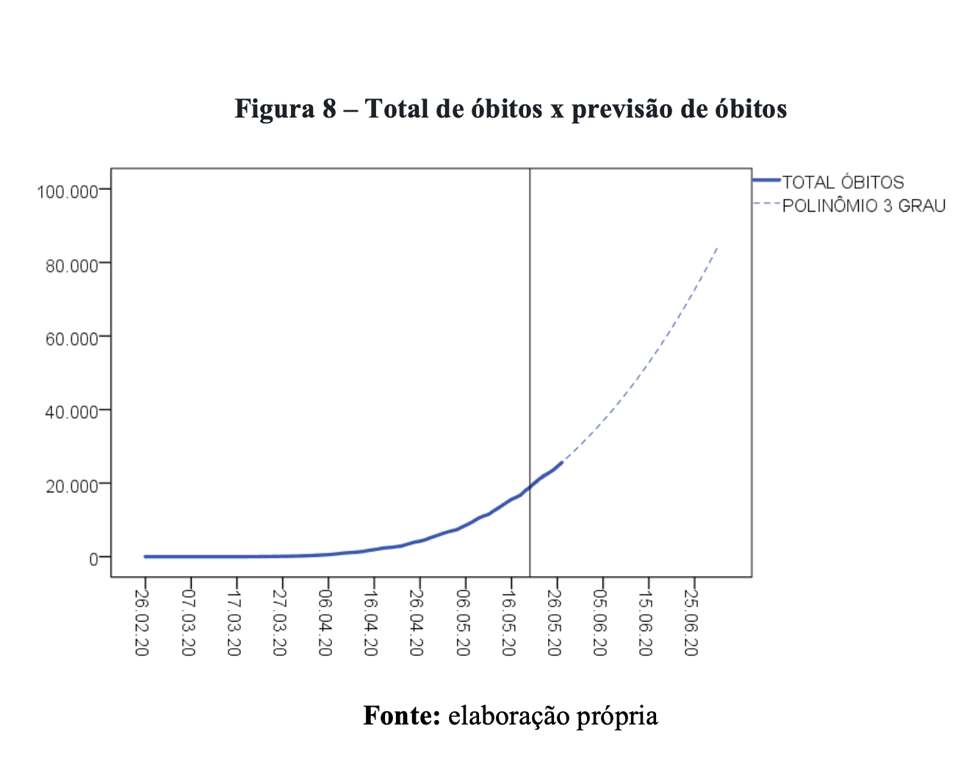
A linha vertical preta indica a data limite em que os dados foram utilizados para realizar a previsão. A curva azul sólida representa o total de óbitos acumulados por COVID-19 no Brasil. Por sua vez, a linha pontilhada ilustra exatamente o movimento previsto pelo modelo polinomial do terceiro grau. Os dados de 27/05/2020 foram divulgados: 25.598 óbitos. O modelo indicou 25.665 mortes. A diferença foi de 0,26%. Como bem colocado pelo comentarista, esses modelos são adequados para previsões de curto prazo.
Por fim, gostaríamos de ressaltar que nosso objetivo no artigo original não é apresentar um modelo de previsão. O intuito não foi utilizar o modelo polinomial para descrever o processo gerador da série. Nossa meta foi melhor compreender a dinâmica longitudinal dos dados em perspectiva comparada. E, para isso, examinamos a variação da quantidade de óbitos acumulados em função do tempo. A regressão polinomial é uma ferramenta muito mais simples do que, por exemplo, um modelo auto regressivo integrado de médias móveis (ARIMA).
CRÍTICA 4
A seguinte afirmação está errada: “Em estatística, um dos pressupostos de um modelo bem ajustado é que o erro tenha média zero (ver linha pontilhada preta na Figura 4)”. Uma maneira simples de ver isso é que você poderia colocar um polinômio de grau elevado que oscilaria loucamente, mas passaria exatamente pelos pontos. Isso, porém, não seria um modelo bem ajustado simplesmente por não corresponder à realidade. O que se deve verificar não é a média, mas a soma dos quadrados das diferenças, ponderada pelas incertezas e considerando os graus de liberdade no ajuste - tudo isso levando-se em conta o critério de verossimilhança da curva utilizada.
Resposta:
Existem várias formas de avaliar a qualidade do ajuste de um modelo estatístico. Em séries temporais, por exemplo, podemos avaliar o Erro Absoluto Percentual Médio (mean absolute percentage error - MAPE). Em regressão, uma estimativa muito utilizada é o coeficiente de determinação (r²) que é comumente interpretado como o percentual da variação na variável dependente explicada pela variação do conjunto de variáveis independentes. O r² varia entre 0 e 1. Quanto maior, melhor o ajuste do modelo aos dados. Quanto menor, pior o ajuste. Todavia, essa estimativa tem várias limitações e, por isso, deve ser interpretada em conjunto com outras informações. Talvez um exemplo nos ajude a melhor compreender como a análise gráfica pode ser mais informativa do que a avaliação isolada de um ou outro parâmetro estatístico. A Figura 9 ilustra o famoso quarteto de Anscombe (1973).
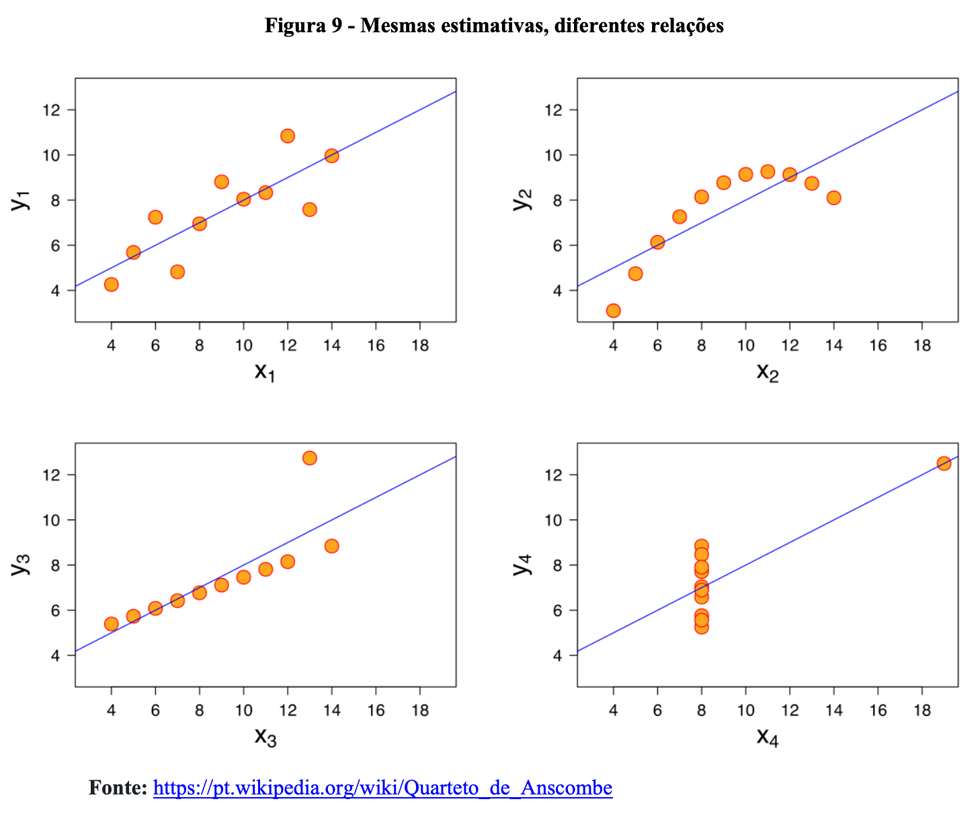
Para todos as figuras, temos o mesmo r2: 0,667. No entanto, o padrão observado entre as variáveis é totalmente diferente. A utilização de uma reta, por exemplo, para descrever a relação curvilinear entre X2 e Y2 é inadequada e ineficiente. Da mesma forma, não existe relação entre X4 e Y4. O coeficiente positivo de regressão nada informa sobre o processo gerador dos dados.
No texto original, não afirmamos que o erro médio igual a zero é o único parâmetro de análise do ajuste de um modelo. Ele é um dos critérios que devem ser levados em consideração, assim como a soma dos quadrados das diferenças, incertezas e os graus de liberdade, por exemplo. Como a revista é voltada para um público mais amplo, optamos por reportar um procedimento mais simples. Nossa interpretação do erro pode ser encontrada em Kennedy (2009), de que a expectativa do termo de erro tem média zero.
Por fim, em relação ao argumento “um polinômio de grau elevado oscilaria loucamente, mas passaria exatamente pelos pontos”, estamos de acordo com o comentarista. A Figura 10 ilustra esse problema.
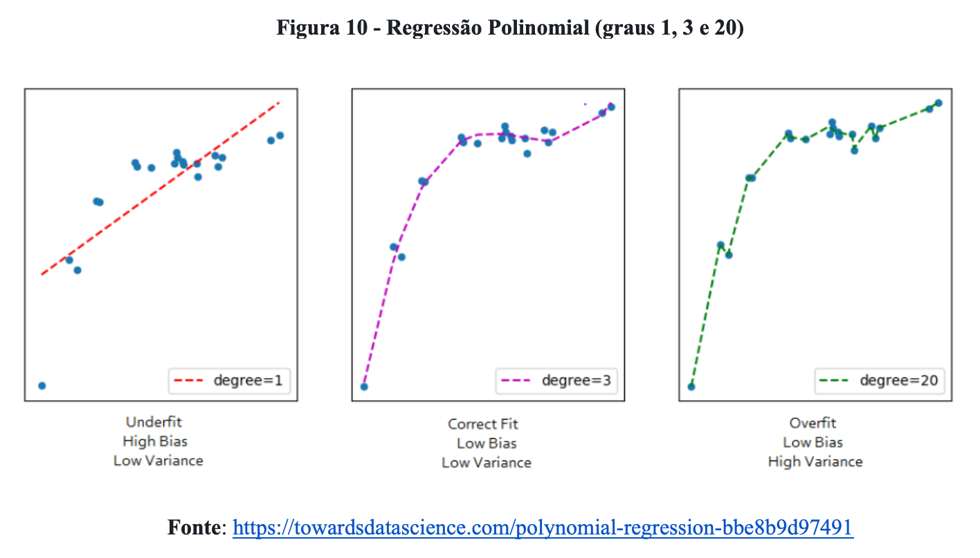
Para essa amostra, a utilização de uma reta, 1º grau, produz um ajuste com forte viés. Por sua vez, a adoção de um modelo cúbico, 3º grau, apresenta baixo viés e baixa variância. Por fim, o emprego de um polinômio elevado, 20º grau, foi capaz de descrever exatamente o comportamento dos dados, mas representa um modelo extremamente complexo e que dificilmente poderá ser utilizado para explicar a realidade.
Considerações à resposta:
O principal problema do artigo é dar ao leitor a impressão de que se tem um modelo matemático de previsão, quando na verdade há apenas o simples ajuste dos dados a uma curva polinomial. Em intervalos de tempo suficientemente curtos, até mesmo uma reta, traçada por dois pontos, tem boa chance de “prever” a posição do terceiro ponto. Isso não se compara a um modelo de equações diferenciais acopladas, como ocorre em modelos epidemiológicos. Como os próprios autores reconhecem, não se pode prever até quando os dados reais acompanharão a curva, já que um polinômio de terceiro grau não é uma curva adequada para extrapolar o comportamento dos dados. Considerando, portanto, a inadequação da curva utilizada, a apresentação do gráfico de resíduos é desnecessária e acaba induzindo o leitor ao erro, já que sugere que existe um grande rigor na escolha da função, e que ela poderia também ser utilizada para fazer previsões.
