O estudo “Evaluation of Hydroxychloroquine or Chloroquine for the Prevention of COVID-19 (COPCOV): A Double-Blind, Randomized, Placebo-Controlled Trial”, publicado recentemente no periódico PLOS Medicine, gerou interpretações controversas no Brasil. Alguns profissionais de saúde têm citado este estudo como "prova conclusiva" da eficácia do medicamento para quimioprofilaxia – isto é, como forma de evitar as complicações trazidas pela infecção com o vírus –, e descrevendo o trabalho como a "redenção" ou "revanche" da hidroxicloroquina no contexto da COVID-19.
Essa interpretação, no entanto, entra em choque com as limitações metodológicas do estudo e o efeito modesto apresentado nos dados.
Este texto utiliza os dados públicos disponibilizados pelos próprios autores do estudo para discutir suas limitações metodológicas, a plausibilidade dos resultados, possíveis vieses e a aplicabilidade prática dos achados. A análise técnica demonstrará que a ideia de que o trabalho representa a “revanche” ou “redenção” da cloroquina/hidroxicloroquina no contexto da COVID-19 é, na melhor das hipóteses, ingênua.
O Gráfico ilusório
No capítulo 5 do livro “Como Mentir Com Estatística”, Darrell Huff explica como manipular o eixo vertical (“y”) de um gráfico pode induzir o leitor a interpretar de modo errôneo os dados apresentados. Por exemplo, os gráficos abaixo mostram a diferença de altura entre dois irmãos, um com 1,80 m e outro com 1,78 m:
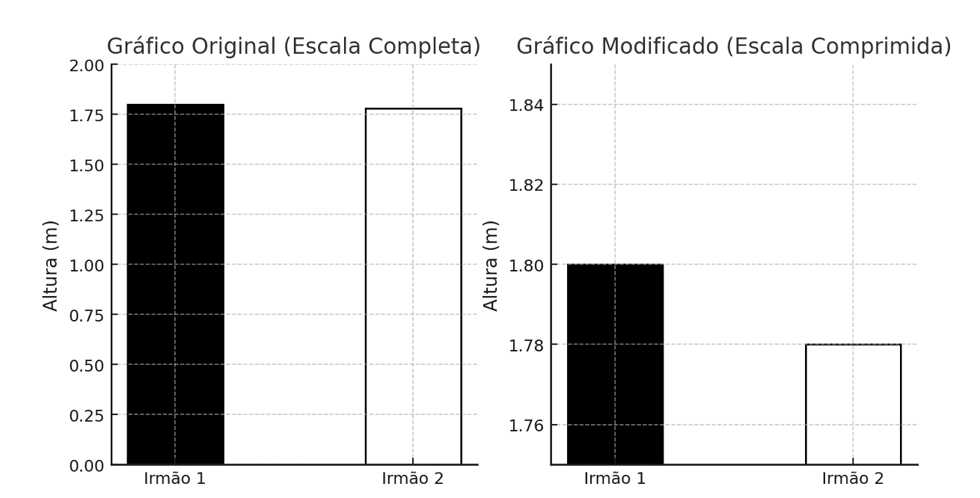
Note que são os mesmos dados em ambas as figuras. Porém, no gráfico da esquerda os irmãos parecem ter quase a mesma altura (e, de fato, a diferença entre eles é de apenas 2 cm, ou 1,1%). Mas se decidirmos iniciar o eixo vertical num ponto arbitrário, diferente de zero, podemos fazer essa diferença parecer muito maior, como o segundo gráfico ilustra.
O estudo COPCOV fez algo semelhante. O eixo vertical de um dos gráficos foi ajustado para destacar uma diferença minúscula entre os grupos que tomaram hidroxicloroquina e os que tomaram placebo. Na prática, a redução do risco foi mínima, mas, com o gráfico “esticado,” pareceu algo mais impressionante:
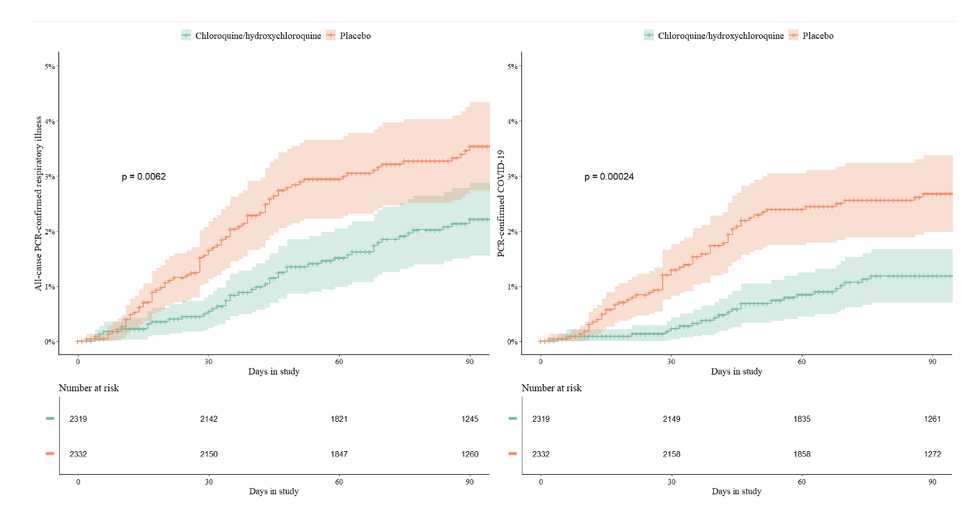
A figura apresenta dois gráficos que comparam o efeito da cloroquina/hidroxicloroquina com o do placebo, ao longo do tempo. O eixo vertical (Y) representa a incidência cumulativa de doenças respiratórias confirmadas por PCR no painel da esquerda e de COVID-19 confirmada por PCR no painel da direita. O eixo horizontal (X) mostra o tempo em dias, ao longo de um período de 90 dias de estudo.
As linhas coloridas nos gráficos representam os diferentes grupos do estudo: a linha verde indica os participantes que receberam cloroquina/hidroxicloroquina, enquanto a linha laranja indica os que receberam placebo. As sombras ao redor dessas linhas correspondem aos intervalos de confiança de 95%, evidenciando a margem de erro e a variabilidade dos dados coletados.
No painel da esquerda, observa-se que a incidência de doenças respiratórias confirmadas por PCR é maior no grupo placebo (linha laranja) do que no grupo que recebeu cloroquina/hidroxicloroquina (linha verde). Trataremos sobre o “valor de p” (o número que aparece “flutuando” sobre as curvas em ambos os gráficos) mais adiante.
No entanto, da mesma forma que fizemos com as alturas dos irmãos, os autores ajustaram o gráfico em uma escala que vai de 0% a 5%, exagerando visualmente a diferença entre os grupos. Em estudos epidemiológicos, gráficos de incidência devem utilizar uma escala completa de até 100%, para contextualizar melhor o impacto real da intervenção. Esse tipo de manipulação visual, portanto, pode ser comparado a observar um objeto através de uma lente de aumento: detalhes mínimos são amplificados e podem distorcer a percepção da realidade. No caso do estudo, ajustar o eixo Y para refletir a escala completa de 100% faz com que a diferença entre os grupos se torne praticamente imperceptível, fornecendo uma visão mais realista dos achados, como mostra a figura abaixo:
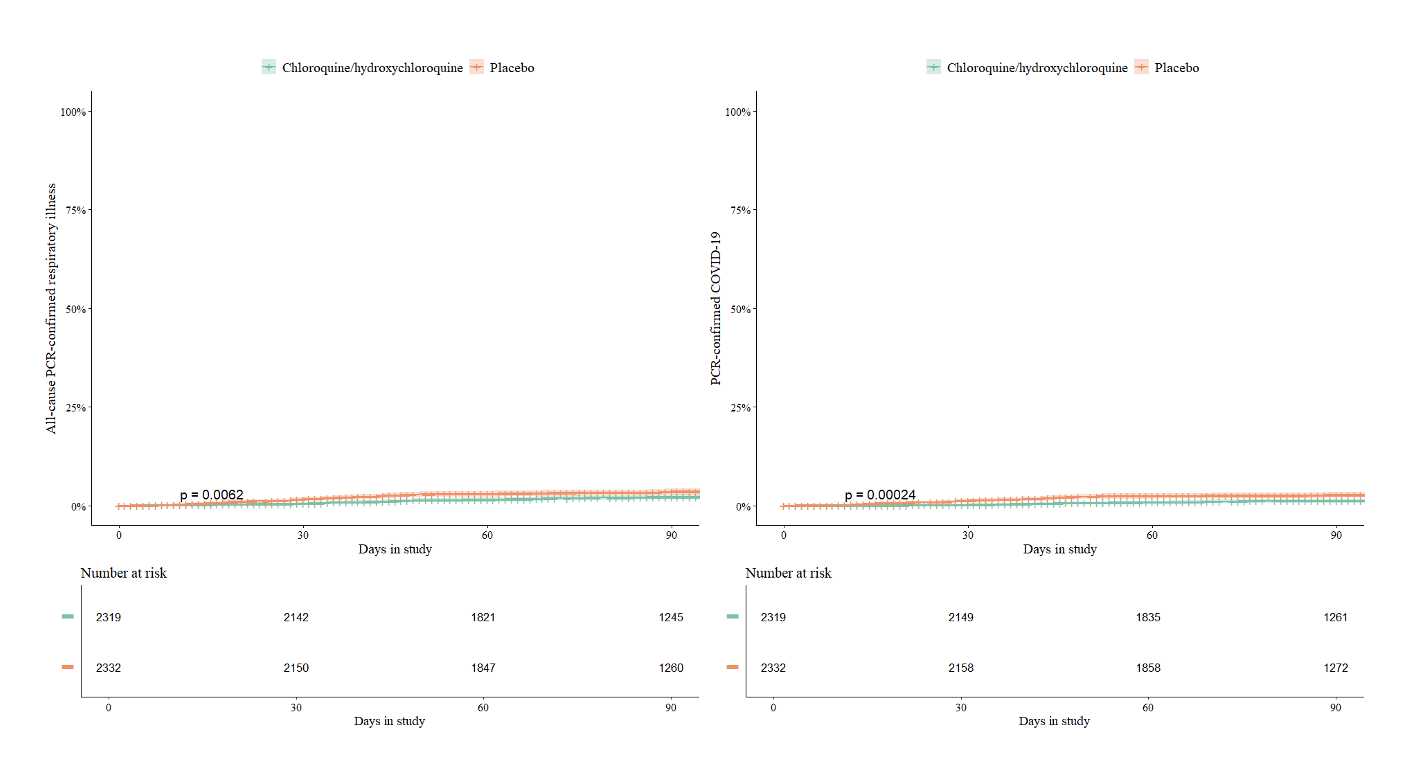
Com essa escala, a diferença quase desaparece, mostrando o verdadeiro impacto (ou a falta dele) da hidroxicloroquina.
Estatísticas
Os autores utilizaram uma técnica estatística chamada "teste exato de Fisher" para calcular os valores de p dos desfechos primários. Grosso modo, o valor de p é uma convenção estatística que ajuda os cientistas a decidir se podem aceitar os resultados encontrados no estudo. De modo geral, se o valor de p for menor que 0,05 (5%), considera-se que é razoável supor que a diferença observada entre os grupos – no caso, placebo e cloroquina – seja real, permitindo que os pesquisadores rejeitem a chamada “hipótese nula” (não existe diferença real) e aceitem a “hipótese experimental” (que há uma diferença concreta entre os grupos: ou, no caso, que tomar cloroquina/hidroxicloroquina fez diferença na saúde dos voluntários). O COPCOV encontrou, para seu desfecho primário – número de casos de COVID-19 com sintomas e confirmados por laboratório – um valor de p de 5,1%. Na “trave”, portanto.
Embora útil em certas situações, o teste exato de Fisher não é adequado para avaliar a eficácia de medicamentos, como a hidroxicloroquina, em ensaios clínicos de COVID-19.
Usar o teste exato de Fisher em um grande estudo como este, com milhares de participantes (quase 5 mil, no total), é tentar usar uma pinça para mover uma pedra gigante. A pinça pode ser perfeita para pegar coisas pequenas, mas é totalmente inadequada para lidar com algo tão grande. Da mesma forma, esse teste é mais recomendado para amostras pequenas e poucos dados.
Além disso, o teste exato de Fisher avalia apenas a associação entre duas variáveis categóricas (por exemplo, tratamento e desfecho), sem permitir ajustes para outras variáveis que possam influenciar os resultados, como idade, comorbidades e sexo. Para realizar uma análise mais adequada dos dados, é necessário incluir essas covariáveis em um modelo estatístico mais sofisticado, como o modelo de Poisson.
A partir do código disponível em https://github.com/jwatowatson/COPCOV/tree/main, fica claro que os autores utilizaram o modelo de Poisson para calcular outra estatística, o risco relativo (RR) do desfecho primário. Se o mesmo modelo tivesse sido empregado para calcular o valor de p, o seguinte resultado teria sido obtido:
Para quem recebeu cloroquina ou hidroxicloroquina, o RR foi de 0,85, com um intervalo de confiança de 95% (ou seja, a margem de erro) entre 0,71 e 1,01, e um valor de p de 0,063 (6,3%). Em resumo, o efeito não foi estatisticamente significativo.
“Risco Relativo”, nesse caso, é a proporção entre o risco de contrair COVID-19 observado entre os pacientes que tomaram cloroquina/hidroxicloroquina e os que tomaram placebo. Esses números são iguais aos apresentados no estudo, mas o valor de p é um pouco maior do que o limite usual de 0,05, o que significa que o resultado não é forte o bastante para que se afirme a presença de um efeito real.
Quando incluímos a idade dos participantes no modelo, os resultados mudam mais:
O RR para o tratamento não se alterou, mas o valor de p ficou em 0,060, ainda não significativo.
A despeito disso, a idade teve um impacto importante: cada ano a mais de vida reduziu a chance de ter a doença em 2%, com um valor de p significativo (menor que 0,001). Isso mostra que a idade realmente fez diferença.
Esses dados podem ser influenciados pelas características da amostra. A média de idade dos participantes era de 32 anos, e apenas 119 dos 4.653 participantes tinham 60 anos ou mais. A idade máxima observada foi de 71 anos, mas isso foi registrado em apenas um indivíduo. Em outras palavras, o estudo pode não ser representativo o suficiente para aplicar suas conclusões a populações mais vulneráveis, como idosos, que são os mais afetados pela COVID-19. Isso enfraquece a confiança geral na relevância prática dos resultados, especialmente quando se trata de entender como o tratamento funcionaria em grupos de maior risco.
Falta de ajustes
A correção de Bonferroni é uma técnica estatística utilizada quando há múltiplas comparações em um estudo. Imagine que você está jogando dardos num alvo. A cada arremesso, aumentam suas chances de acertar na mosca, por sorte. Quanto mais dardos você lançar, maior a probabilidade de um acerto ser simples acaso, e não prova de habilidade. No contexto de modelos estatísticos, quando testamos múltiplas variáveis ao mesmo tempo (como diferentes tratamentos ou características, como sexo), cada nova comparação aumenta a chance de obter um resultado significativo apenas por acaso.
A correção de Bonferroni ajusta os valores de p, dividindo o nível de significância (geralmente 0,05, ou 5%) pelo número de comparações feitas. Isso torna os critérios para significância mais rigorosos, reduzindo as chances de chegar a conclusões incorretas com base em resultados que poderiam ser fruto do acaso.
Sem a adição de variáveis como idade e sexo e sem a correção de Bonferroni, os autores observaram uma diferença quase significativa entre os grupos de tratamento e placebo sobre o desfecho de COVID-19 confirmado por PCR. Ou seja, sem considerar outras variáveis que poderiam influenciar o resultado, o modelo mostrava que o tratamento parecia mais eficaz do que o placebo. No entanto, ao ajustarmos o modelo com a idade, o sexo dos participantes e aplicando a correção de Bonferroni, o valor de p ajustado foi 0,999.
Riscos desproporcionais
O Modelo de Cox é uma técnica estatística amplamente utilizada em estudos que analisam o tempo até um evento acontecer, como o tempo até um paciente desenvolver uma doença (como a COVID-19), ou se recuperar.
O gráfico de Kaplan-Meier, apresentado na Figura 3 do artigo original (aquele em que os autores comprimiram o eixo vertical) é útil para descrever a distribuição dos desfechos ao longo do tempo. No entanto, ele não fornece uma medida quantitativa do risco entre os grupos. Para isso, seria preciso utilizar o Modelo de Cox. Embora os autores não tenham entrado nesse mérito, este modelo poderia ter sido empregado para calcular a razão de risco (Hazard Ratio) e entender a relação entre os grupos de tratamento e o risco de um desfecho específico.
Porém, antes de aplicar o Modelo de Cox, é crucial verificar se os pressupostos que sustentam o modelo são atendidos. O primeiro pressuposto é a independência dos tempos de sobrevida. Isso significa que o número de dias até um participante contrair COVID-19 não deve influenciar o número de dias até que outro participante contraia a doença. No COPCOV, isso é relevante porque os participantes estavam espalhados em diferentes locais e não tinham interação direta, o que sugere que este pressuposto foi atendido.
O segundo pressuposto é censura não informativa. “Censura”, no contexto da pesquisa clínica, acontece, por exemplo, quando alguns participantes saem do estudo antes do final. Para que os resultados sejam confiáveis, o eventual abandono do estudo por alguns participantes não deve estar ligado ao risco de contrair COVID-19. Se um participante sai do estudo porque mudou de cidade (e não porque ficou doente demais para continuar), isso não afeta os resultados. Segundo os autores, esse pressuposto também foi considerado atendido.
O terceiro pressuposto, e talvez o mais crítico, é a proporcionalidade dos riscos. Esse pressuposto significa que a diferença no risco de contrair COVID-19 entre o grupo que tomou hidroxicloroquina e o que tomou placebo deve ser constante ao longo do tempo. Se, por exemplo, o risco de um grupo ser mais afetado mudasse durante o período do estudo, o Modelo de Cox não forneceria resultados confiáveis.
Para testar a suposição de proporcionalidade dos riscos, existem duas abordagens principais. A primeira é examinar o gráfico de Kaplan-Meier, que permite visualizar as curvas de sobrevida dos diferentes grupos. Se as curvas mantiverem uma distância constante e paralela durante o período de observação, isso sugere que os riscos são proporcionais. No entanto, a Figura 3 do estudo mostra que as curvas se cruzam sutilmente no início, o que levanta uma preocupação.
Apesar de o cruzamento das curvas ser discreto e ocorrer apenas no começo do período de observação, é prudente realizar uma análise mais aprofundada para confirmar ou refutar essa violação. Uma técnica comumente utilizada para isso é a análise de resíduos de Schoenfeld. Ela examina se o comportamento dos dados ao longo do tempo segue o padrão esperado. No estudo COPCOV, essa análise revelou uma tendência nos dados, com um valor de p significativo (0,0189), indicando que a suposição de proporcionalidade dos riscos foi violada. Isso significa que a razão de risco entre os grupos não permaneceu constante (os riscos não foram proporcionais), tornando o Modelo de Cox inadequado.
Dado esse cenário, voltamos ao ponto do valor de p observado na primeira figura desse artigo. Apesar de ela sugerir uma diferença quase significativa entre os grupos, o valor de p apresentado não pode ser interpretado como válido. Quando a suposição de proporcionalidade dos riscos é violada, qualquer conclusão derivada do Modelo de Cox (e do gráfico de Kaplan-Meier) deve ser reconsiderada.
Impacto e plausibilidade
Vamos, por um momento, ignorar as inadequações descritas e aceitar os dados apresentados na publicação como válidos.
Embora a eficácia da cloroquina/hidroxicloroquina detectada pelo estudo tenha sido descrita como “moderada” pelos autores, os números contam uma história diferente. A redução absoluta do risco (ARR) foi de apenas 1,9%, o que significa que seria necessário tratar 53 pessoas com cloroquina ou hidroxicloroquina para prevenir um único caso de COVID-19 sintomática. Em termos simples, o Número Necessário para Tratar (NNT) de 53 sugere que o benefício prático desse tratamento é extremamente limitado, especialmente quando consideramos os recursos de saúde e os riscos associados aos medicamentos.
Outro ponto importante é que o trabalho não encontrou casos graves de COVID-19 ou hospitalizações. Todos os casos observados foram leves ou moderados, e não houve diferença significativa na gravidade dos sintomas ou na necessidade de hospitalização entre os grupos. Além disso, a mortalidade não foi analisada como desfecho, provavelmente porque a maioria dos participantes era de adultos jovens e saudáveis, com baixo risco de complicações graves. Isso já levanta dúvidas sobre o impacto do tratamento em populações mais vulneráveis.
A ideia de que a hidroxicloroquina teria um efeito profilático isolado – prevenindo apenas infecções sintomáticas, sem reduzir hospitalizações ou mortes – enfraquece a noção de uma relação causal consistente. De acordo com os critérios científicos para estabelecer causalidade, um tratamento eficaz deve mostrar benefícios de forma coerente e consistente em diferentes desfechos relacionados, não apenas em um ponto específico. Por exemplo, seria esperado que um medicamento preventivo eficaz reduzisse não apenas o número de pacientes sintomáticos, mas também mostrasse algum impacto em pacientes já doentes.
Considere, por exemplo, os antivirais usados como profilaxia pré-exposição (PrEP) para o HIV. Esses medicamentos demonstram eficácia preventiva, reduzindo o risco de infecção por HIV, em pessoas saudáveis, de forma consistente. Além de prevenir a infecção, esses mesmos antivirais também são eficazes no tratamento, controlando a replicação viral em pessoas infectadas, reduzindo a carga viral e prevenindo o avanço para a Aids. Ou seja, os antivirais apresentam um impacto coerente tanto na prevenção quanto no controle de formas graves da infecção.
Em doenças como a COVID-19, que apresentam diferentes níveis de gravidade, não é comum que uma intervenção profilática previna apenas os sintomas leves, sem ter efeito nos desfechos mais graves, como hospitalizações ou mortes. Isso torna a alegação de eficácia profilática isolada da hidroxicloroquina pouco plausível e fragiliza a interpretação dos resultados como “prova” de eficácia.
Para ilustrar o impacto limitado: mesmo se assumirmos uma taxa de letalidade da doença de 2,5% no início da pandemia (ou seja, 2,5% dos casos sintomáticos levariam à morte), o tratamento com hidroxicloroquina teria um impacto pouco relevante na mortalidade. Cerca de 2.105 pessoas precisariam ser tratadas para prevenir uma única morte. Considerando os custos, os recursos necessários e os possíveis efeitos adversos da hidroxicloroquina, o impacto é praticamente nulo. Portanto, interpretar este estudo como uma evidência sólida da eficácia da hidroxicloroquina é uma extrapolação otimista e imprecisa.
A meta-análise
Um ponto final, mas não menos importante, é a revisão dos estudos incluídos na meta-análise que os autores fizeram ao final do artigo em questão. Identificamos erros de digitação nos valores de efeito e nos intervalos de confiança reportados. Por exemplo, no estudo de Llanos-Cuentas (2023), onde a meta-análise reportou RR = 1,48 (95% CI 0,38–5,71), o estudo original mostra RR = 1,69 (95% CI 0,41–7,11).
Esses erros podem comprometer a precisão e validade dos resultados agregados da meta-análise, prejudicando a confiabilidade das conclusões. Uma revisão detalhada dos dados originais de cada estudo e o recálculo dos tamanhos de efeito e intervalos de confiança são necessários para garantir que as conclusões sejam precisas. Por fim, os autores incluíram os resultados de seus próprios estudos na meta-análise. Como já discutido, os valores dos efeitos e intervalos de confiança precisam ser ajustados adequadamente, para então serem incorporados novamente.
A falta de dados abertos na maioria dos estudos incluídos dificulta uma verificação mais detalhada dos cálculos de risco relativo (RR), limitando a transparência e a reprodutibilidade da análise. Isso destaca a necessidade de um processo mais rigoroso na inclusão de dados na meta-análise, para garantir que os resultados reflitam de forma justa a eficácia do tratamento investigado.
Considerações finais
A análise crítica do estudo COPCOV revela importantes limitações que comprometem a robustez de suas conclusões sobre a eficácia da hidroxicloroquina como profilaxia para a COVID-19. A manipulação da visualização de dados, o uso inadequado de testes estatísticos e a violação das suposições do Modelo de Cox enfraquecem a confiança nos resultados apresentados.
Ainda que fizéssemos “vista grossa” a tudo isso, o impacto prático da intervenção seria mínimo, com uma baixa redução absoluta do risco e um elevado número necessário para tratar, o que não justifica a aplicação em larga escala. A ausência de efeitos consistentes em desfechos graves e a falta de plausibilidade científica para um efeito preventivo isolado destacam a fragilidade da hipótese de causalidade.
A inclusão de estudos com erros de digitação e a dificuldade de verificação, devido à falta de dados abertos, representam graves limitações da meta-análise agregada ao estudo. Assim, qualquer extrapolação desses achados para justificar o uso generalizado da hidroxicloroquina como profilaxia, ou pior, como uma forma anacrônica de justificar erros cometidos no passado, é excessivamente otimista e cientificamente questionável.
Luiz Gustavo de Almeida é Coordenador de Educação Científica do Instituto Questão de Ciência
André Bacchi é professor adjunto de Farmacologia da Universidade Federal de Rondonópolis. É divulgador científico e autor dos livros "Desafios Toxicológicos: desvendando os casos de óbitos de celebridades" e "50 Casos Clínicos em Farmacologia" (Sanar), "Porque sim não é resposta!" (EdUFABC), "Tarot Cético: Cartomancia Racional" (Clube de Autores) e “Afinal, o que é Ciência?...e o que não é. (Editora Contexto).
